The Högbom Algorithm

Consider a sky containing only isolated point sources. In the dirty map, each appears as a copy of the dirty beam, centred on the source position and scaled by its strength. However, the maxima in the map do not strictly correspond to the source positions, because each maximum is corrupted by the sidelobes of the others, which could shift it and alter its strength. The least corrupted, and most corrupting, source is the strongest. Why not take the largest local maximum of the dirty map as a good indicator of its location and strength? And why not subtract a dirty beam of the appropriate strength to remove to a great extent the bad effects of this strongest source on the others? The new maximum after the subtraction now has a similar role. At every stage, one writes down the co-ordinates and strengths of the point sources one is postulating to explain the dirty map. If all goes well, then at some stage nothing (or rather just the inevitable instrumental noise) would be left behind. We would have a collection of point sources, the so called CLEAN components, which when convolved with the dirty beam give the dirty map.

One could exhibit this collection of point sources as the solution to the deconvolution problem, but this would be arrogant, since one has only finite resolution. As a final gesture of modesty, one replaces each point source by (say) a gaussian, a so called ``CLEAN" beam, and asserts that the sky brightness, convolved with this beam, has been found.

This strategy, which seems so reasonable today, was a real breakthrough in 1974 when proposed by J. Högbom. Suddenly, one did not have to live with sidelobes caused by incomplete 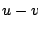$u-v$ coverage. In fact, the planning for new telescopes like the VLA must have taken this into account- one was no longer afraid of holes.