


Next: Maximum Entropy
Up: CLEAN
Previous: The Behaviour of CLEAN
Contents
Apart from the difficulties with extended
sources, CLEAN as described above is an inherently slow procedure. If 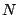 is the number of pixels, subtracting a single source needs of the order of
is the number of pixels, subtracting a single source needs of the order of
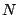 operations. This seems a waste when this subtraction is a provisional,
intermediate step anyway! B.G. Clark had the insight of devising a faster
version, which operates with a truncated dirty beam, but only on those
maxima in the map strong enough that the far, weak sidelobes make little
difference. Once these sources have been identified by this rough CLEAN
(called a ``minor cycle''), they are subtracted together from the full map
using an fast fourier transform (FFT) for the convolution, which takes
only
operations. This seems a waste when this subtraction is a provisional,
intermediate step anyway! B.G. Clark had the insight of devising a faster
version, which operates with a truncated dirty beam, but only on those
maxima in the map strong enough that the far, weak sidelobes make little
difference. Once these sources have been identified by this rough CLEAN
(called a ``minor cycle''), they are subtracted together from the full map
using an fast fourier transform (FFT) for the convolution, which takes
only 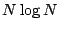 operations. This is called the ``major cycle''. The new
residual map now has a new definition of ``strong'' and the minor cycle is
repeated.
operations. This is called the ``major cycle''. The new
residual map now has a new definition of ``strong'' and the minor cycle is
repeated.
A more daring variant, due to Steer, Dewdney, and Ito, (hence SDI CLEAN)
carries out the minor cycle by simply identifying high enough maxima,
without even using CLEAN, which is kept for the major cycle. Other efforts
to cope with extended sources go under the name of ``multiresolution
CLEAN''. One could start with the inner part of the 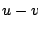 plane and do a
CLEAN with the appropriate, broader dirty beam. The large scale structure
thus subtracted will hopefully now not spoil the next stage of CLEAN at a
higher resolution, i.e using more of the
plane and do a
CLEAN with the appropriate, broader dirty beam. The large scale structure
thus subtracted will hopefully now not spoil the next stage of CLEAN at a
higher resolution, i.e using more of the 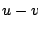 plane.
plane.



Next: Maximum Entropy
Up: CLEAN
Previous: The Behaviour of CLEAN
Contents
NCRA-TIFR
![]() plane and do a
CLEAN with the appropriate, broader dirty beam. The large scale structure
thus subtracted will hopefully now not spoil the next stage of CLEAN at a
higher resolution, i.e using more of the
plane and do a
CLEAN with the appropriate, broader dirty beam. The large scale structure
thus subtracted will hopefully now not spoil the next stage of CLEAN at a
higher resolution, i.e using more of the ![]() plane.
plane.