The co-planar approximation of Eq. 14.1.1 for a pointing direction
given by ![]() can be written as
can be written as
![]() represents the single dish observation in the
direction (
represents the single dish observation in the
direction (![]() ) and is just the convolution of the primary beam
with the source brightness distribution, exactly as expected
intuitively. Extending the intuition further, as is done in mapping
with a single dish, we need to scan the source around
) and is just the convolution of the primary beam
with the source brightness distribution, exactly as expected
intuitively. Extending the intuition further, as is done in mapping
with a single dish, we need to scan the source around ![]() with
the interferometer, which is equivalent to scanning with a single dish
with a primary beam of the size of the synthesized beam of the
interferometer. Then Fourier transforming
with
the interferometer, which is equivalent to scanning with a single dish
with a primary beam of the size of the synthesized beam of the
interferometer. Then Fourier transforming
![]() with
respect to (
with
respect to (![]() ), assuming that
), assuming that ![]() is symmetric, one gets, from
Eq. 14.3.9
is symmetric, one gets, from
Eq. 14.3.9
Image of the sky can now be made using the full visibility data set
(made using the Eq. 14.3.10). However, this involves the
knowledge of Fourier transform of the sky brightness distribution,
which in-turn is approximated after deconvolution. Hence, in practice
one uses the MEM based image recovery where one maximizes the entropy
given by
| (14.3.11) |
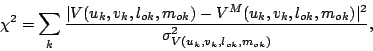 |
(14.3.12) |
The operation of primary beam correction on the residual image is
understood by the following argument: For any given pointing, an
interferometer gathers radiation within the primary beam. In the
image plane then, any feature, outside the range of the primary beam
would be due to the side lobes of the synthesized beam and must be
suppressed before computation of ![]() and this is achieved
by primary beam correction, which essentially divides the image by
gaussian which represents the main lobe of the antenna radiation
pattern.
and this is achieved
by primary beam correction, which essentially divides the image by
gaussian which represents the main lobe of the antenna radiation
pattern.
This approach (rather than joint deconvolution) has several advantages.
The most important advantage that one gets by MEM reconstruction is
that the deconvolution is done simultaneously on all points. That
this is an advantage over joint-deconvolution can be seen as follows:
If a point source at the edge of the primary beam is sampled by 4
different pointings of the telescope, this procedure would be able to
use 4 times the data on the same source as against data from only one
pointing in joint-deconvolution (where deconvolution is done
separately on each pointing). This, apart from improvement in the
signal-to-noise ratio also benefits from a better ![]() -coverage
available.
-coverage
available.
Flexible software for performing Mosaic-ed observations is one of the primary motivation driving the AIPS++ project in which algorithms to handle mosaic-ed observations would be available in full glory.