Propagation Through a Smooth Ionosphere

Figure 16.1: Propagation through a plane parallel ionosphere

For an interferometer, there are two quantities of interest (i) the delay difference between the signals reaching the two arms of the interferometer ( $\delta T\ =\ \Delta T_1 - \Delta T_2$), where $\Delta T_1$ and $\Delta T_2$ are the propagation delays for the two arms of the interferometer, and (ii) the phase difference between the signals reaching the two arms of the interferometer ( $\delta \phi\ = \ 2\pi/\lambda (\Delta L_1 - \Delta L_2$), where $\Delta L_1$ and $\Delta L_2$ are the excess path lengths for the two arms of the interferometer. Generally $\delta T$ is small compared to the coherence bandwidth of the signal and can be ignored to first order, however $\delta \phi$ could be substantial.

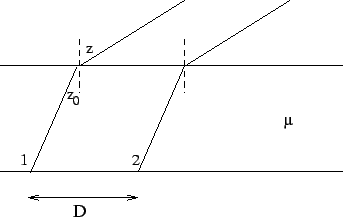
In a homogeneous plane parallel ionosphere with refractive index $\mu$ (see Figure 16.1), we have from Snell's law $\mu\sin(z_0)=\sin(z)$. The observed geometric delay is $\tau_g = \mu D\sin(z_0)/c$, since the group velocity is $c/\mu$. From Snell's law therefore, $\tau_g = D\sin(z)/c$, the same as would have been observed in the absence of the ionosphere. A homogeneous plane parallel ionosphere hence produces no net effect on the visibilities, even though the apparent position of the source has changed. In the case where the interferometer is located outside the slab, there is neither a change in the apparent position nor a change in the phase, as is obvious from the geometry. This entire analysis holds for a stratified plane parallel ionosphere (since it is true for every individual plane parallel layer). However, in the real case of a curved ionosphere, with a radial variation of electron density, then neither the change in the apparent position nor $\delta \phi$ are zero even outside the ionosphere. Effectively, the direction of arrival of the rays from the distant source appears to be different from the true direction of arrival (as illustrated in Figure 16.2) and unlike in the plane parallel case this is not exactly canceled out by the change in the refractive index. If $\Delta\theta$ is the difference between the true direction and apparent directions of arrival, then one can compute that

Figure 16.2: Propagation through a curved ionosphere

$$\Delta \theta = { A \sin(z_0) \over r_0 } \int_0^\infty {\alpha^2 \mu(h) dh \over (1 - \alpha^2 \sin^2(z_0))}.$$ (16.3.5)

where $z_0$ is the observed zenith angle, $r_0$ is the radius of the earth, $h$ is the height above the earth's surface and, $\mu(h)$ is the refractive index at height $h$, and $A$ is a constant. For baseline lengths typical of the GMRT, this value is the same for both arms of the baseline. If the baseline has UV co-ordinates (u,v), then the phase difference due to the apparent change in the source position is given by

$$\Delta \phi = 2\pi (u\Delta \theta_{EW}\ +\ v\Delta \theta_{NS}).$$

Typical values for some of the ionospheric prorogation effects that we have been discussing are given in Table 16.1.

Table 16.1: Typical numerical values of various ionospheric effects

	Max. Val	Min Val	Freq. Dependence
	(Day)	(Night)
TEC	$5\times10^{13}$ cm$^{-2}$	$5\times10^{12}$ cm$^{-2}$	-
Group Delay	12  $\mu$sec	1.2  $\mu$sec	$\nu^{-2}$
Excess Path	3500 m	350 m	$\nu^{-2}$
Phase Change	7500 rad	750 m	$\nu^{-2}$
Phase Fluctuation	$\pm 150$ rad	$\pm15$ rad	$\nu^{-2}$
Mean Refraction	$6^{'}$	$0.6^{'}$	$\nu^{-2}$
Faraday Rotation	15 cycles	1.5 cycles	$\nu^{-2}$