Basic Block Diagram of a Pulsar Receiver

Figure 17.1: Block diagram of a typical pulsar receiver

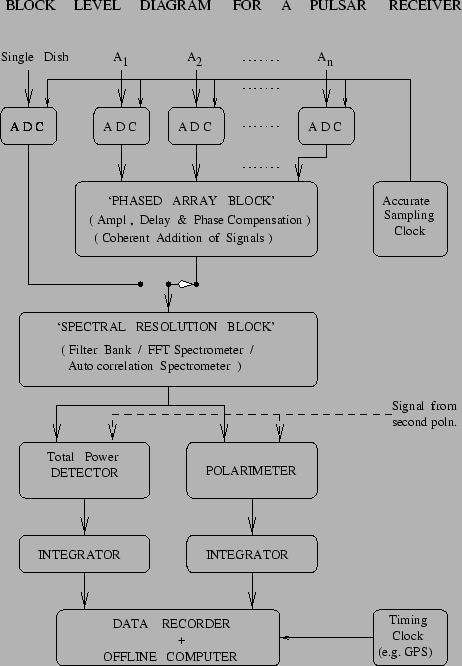
Incorporating the above requirements into a realistic set-up for pulsar observations leads to the following block level diagram for pulsar observations (see Fig 17.1). In a modern radio telescope, most of the processing of the signals is carried out in the digital domain, after down conversion to a baseband signal (of bandwidth $B$). Hence the first block is an analog to digital convertor (ADC), which is run on an accurate and controlled sampling clock. For multi-element or array telescopes, the signals from the different elements need to be phased. This involves proper adjustments of amplitude, delay and phase of the signals (see chapter 6). The output of this block is the phased array signal which goes to the `Spectral Resolution Block'. For a single dish telescope, the signal comes directly from the sampler to this block. This block produces the multiple narrow-band channels from the single broad-band data. This can be achieved using a filter bank or a FFT spectrometer or an auto-correlation spectrometer. The output is a baseband voltage signal for each of $N_{ch}$ frequency channels, sampled at the Nyquist rate. For a multi-element telescope, the location of this block and the Phased Array block can be interchanged, in part or in whole. For example, at the GMRT, the integer sample delay correction is done before the FFT; the fractional sample delay correction and the phase correction is done in the last stage of the FFT and the addition of the signals is done in a separate block located after the FFT. Note that for incoherent phased array operation to be possible, the addition of the signals MUST be after the spectral resolution block, because the square law detection has to be carried out before the incoherent addition can be done.

The second orthogonal polarisation from the telescope is also processed similarly till the output from the spectral resolution block. These outputs can then be given to two different kinds of processors. The first is a total power adder that simply adds the powers of the signals in the two polarisations to give a measure of the total intensity from the telescope as a function of time and freqency. The second is a polarimeter that takes the voltage signals from the two polarisations and produces the four Stokes parameters, as a function of time and frequency. The data from the incoherent phased array, for example, can only be put through the total power path. The outputs from these two processors are then put through an adder that integrates the data to the required time constant, $\tau_{s}$. The final output going to the recorder then is either one (total intensity mode) or four (polarimetry mode) signals each containing $N_{ch}$ frequency channels coming at the rate of $1/\tau_{s}$ samples per second. The net data rate into the recorder is then $N_{ch}/\tau_{s}$ samples per second for the total intensity mode and four times as much for the polarimetry mode. As an example, if data from 256 spectral channels is being acquires with a time constant of 0.25 millisec, the data rate is 1 mega samples per second for the total intensity mode. If one sample is stored as a two byte word, we can see that a storage space of 1 gigabyte would get filled with about 2 minutes of data! In cases where the data rate going into the recorder in the above set-up is difficult to handle for storage or off-line processing, special purpose hardware to do some of the processing on-line can also be used. Typical examples of such processing would be on-line dedispersion, on-line folding at the pulsar period and on-line gating of the data (to pass on only some region of each pulsar period that is around the on-pulse region). Each of these techniques reduces the net data rate so that it can be comfortably acquired and further processed off-line. The choice of the processing technique depends on the scientific goals of the observations.