Computing Reflector Antenna Radiation Patterns

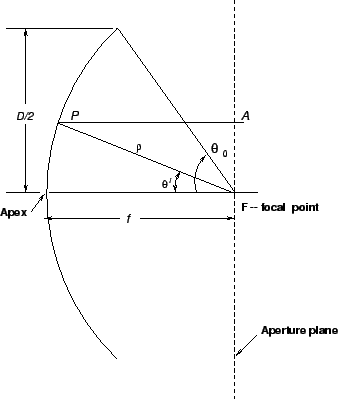
Reflector antenna radiation patterns are determined by a number of factors, but the most important ones are the radiation pattern of the feed antenna and the shape of the reflector. Parabolic reflectors have the unique feature that all path lengths from the focal point to the reflector and on to the aperture plane are the same. As shown in Figure 19.1,

$$FP + PA = {\rho} + {\rho}{\cos{\theta}'}$$

$$= {\rho}(1 + {\cos{\theta}'})$$ (19.4.3)

$$= 2f,$$

since the parabola is described in polar form by, ${\rho}(1 + {\cos{\theta}'}) = 2f$

Figure 19.1: Geometry for determining the aperture field distribution for a prime focus parabolic antenna.

When the reflector dimensions are large compared to the wavelength, geometrical optics principles can be used to determine the power distribution in the aperture plane. If the feed pattern is azimuthally symmetric, then the normalized far-field radiation pattern of reflector depends on

1. ${\pi}u = k\ a\ {\sin{\theta}}$, where $a$ is the radius of the aperture, $k = 2{\pi}/{\lambda}$, and ${\theta}$ is the angle subtended by the far-field point with respect to the parabola's focal axis
2. The feed taper,$C$ [4],[5], which is defined as the amplitude of the feed radiation pattern at the rim of the parabolic reflector relative to the maximum value (assumed to be along the parabola axis). (Note that in standard power plots of radiation patterns (in dB), the edge taper ${T_{E}}$ is related to C by ${T_{E}} = 20 {\log{C}}$).
3. The focal length $f$ which determines how the power from the feed is spread over the aperture plane. If $\tilde{g}(\theta^\prime)$ is the radiation pattern of the feed, $r$ is distance in the aperture plane, and $g(r)$ is the power density in the aperture plane, then we have
   

   $$g(r)\ dr = \tilde{g}(\theta^\prime)\ d\theta^\prime,~{\rm i.e.}~ g(r) = \tilde{g}(\theta^\prime)\ {d\theta^\prime\over dr}$$ (19.4.4)

   
   
   and from Figure 19.1 we have
   

   $${d\theta^\prime\over dr} = {2f \over 1 + cos(\theta^\prime)}$$ (19.4.5)

   
   

In Chapter 3 we saw that the far field is in general the Fourier transform of the aperture plane distribution. In the case of azimuthally symmetric distributions, this can be written as

$$F(u) = {\int_{0}^{\pi}{g(q){J_{0}(qu)}q\:dq}}$$

where $F(u)$ is the far field pattern, $q$ is a normalized distance in the aperture plane, $q = {\pi}(r/a)$, $g(q)$ is the feed's pattern projected onto the aperture plane as discussed above. A convenient parameterization of the feed pattern in terms of the taper, $C$ is

$$g{\left( {\frac{r}{a}} \right)} = C+(1-C){\left[1-{\left( {\frac{r}{a}} \right)}^2\right]}^n$$ (19.4.6)

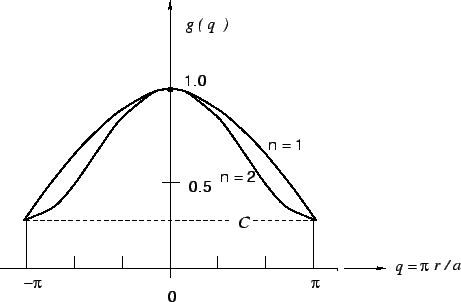
The aperture illuminations corresponding to different values of the parameter $n$ are shown in Figure 19.2. The case $n=0$ corresponds to a uniform aperture distribution.

Figure 19.2: The shape of the aperture illumination as given by eqn 19.4.6 for different values of the parameter $n$.

For uniform illumination the far field pattern is given by

$$F(u) = 2{\cdot}{\frac{J_{1}({\pi}u)}{({\pi}u)}}$$ (19.4.7)

Simple closed-form expressions are available for integer values of $n$. If the above expression $F(u)$ is denoted as ${F_{0}}(u)$, (since $n=0$) the general form for any integer $n$ is given by

$${F_{n}}(u) = {\frac{n+1}{Cn+1}}{\cdot}{\left[ C{F_{0}}(u)+{\frac{1-C} {n+1}}{f_{n}}(u) \right]}$$ (19.4.8)

where,

$${f_{n}}(u) = 2^{n+1}(n+1)!{\frac{J_{n+1}({\pi}u)}{({\pi}u) ^{n+1}}}$$ (19.4.9)

Table 19.1 gives the halfpower beamwidth (HPBW), the first sidelobe level and the taper efficiency (see Section 19.4.1) for various edge tapers $C$ and shape parameter $n$.

Table 19.1: Radiation characteristics of circular aperture

Edge Taper		$n\:=\:1$			$n\:=\:2$
${T_{E}}$		HPBW	Sidelobe	${{\eta}_t}$	HPBW	Sidelobe	${{\eta}_t}$
(dB)	C	(rad.)	level (dB)		(rad.)	level (dB)
-8	0.398	$1.12{{\lambda}/2a}$	-21.5	0.942	$1.14{{\lambda}/2a}$	-24.7	0.918
-10	0.316	$1.14{{\lambda}/2a}$	-22.3	0.917	$1.17{{\lambda}/2a}$	-27.0	0.877
-12	0.251	$1.16{{\lambda}/2a}$	-22.9	0.893	$1.20{{\lambda}/2a}$	-29.5	0.834
-14	0.200	$1.17{{\lambda}/2a}$	-23.4	0.871	$1.23{{\lambda}/2a}$	-31.7	0.792
-16	0.158	$1.19{{\lambda}/2a}$	-23.8	0.850	$1.26{{\lambda}/2a}$	-33.5	0.754
-18	0.126	$1.20{{\lambda}/2a}$	-24.1	0.833	$1.29{{\lambda}/2a}$	-34.5	0.719

From Table 19.1 (see also the discussion in Chapter 3) we find that as the edge-taper parameter $C$ decreases, the HPBW increases, the first sidelobe level falls and the taper-efficiency also decreases. Note that $C$ has to be less than unity since we have assumed a radiation pattern which decreases monotonically with increasing angle from the symmetry-axis (Eqn 19.4.6, Fig 19.2).