Image Formation

An array can be considered as a sampled aperture. When an array is illuminated by a source, samples of the source's wavefront are recorded at the location of the antenna elements. The outputs from the elements can be subjected to various forms of signal processing, where in phase and amplitude adjustments are made to produce the desired outputs. If the voltages from elemental antennas are simply added (as in the phased arrays discussed in Chapter 6), the energy received from a large portion of the sky will be rejected. When the array is illuminated by a point source this gives the beam of the array which is the Fourier transform of the aperture current distribution. A single beam instrument can use only a part of the total available time to observe each beam width of the sky. One can generate multiple independent beams in the sky by amplifying the signals from element separately and combining them with different phase shifts. Such a multiple-beam or image forming instrument can observe different directions in the sky simultaneously.

A simple linear array, which generates a single beam, can be converted to a multiple beam antenna by attaching phase shifters to the output of each element. Each beam to be formed requires one additional phase shifter per element. Thus an $N$ element array needs $N$ squared phase shifters. 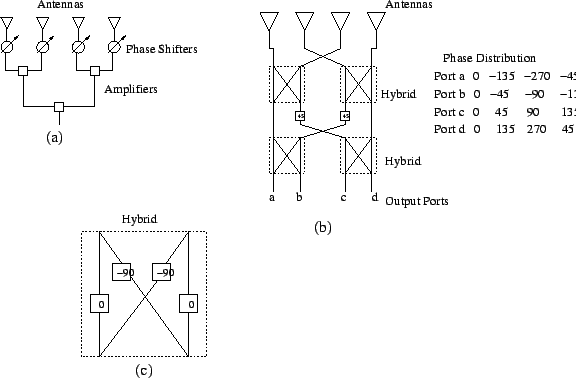Since the formation of a beam is Fourier transforming the aperture distribution, this requirement of $N$ squared phase shifters is very similar to the requirement of $N$ squared multipliers for an $N$ point Fourier transform. Such a network is known as a Blass network (Figure 7.2). Similar to the fast Fourier transform, we also have a Butler beam-forming matrix, which needs only $N{\times}logN$ elements for beam forming. The Butler matrix uses $90^0$ phase-lag hybrid junctions with $45^0$ fixed-phase shifters. Blass and Butler networks for a four-element array are shown in the Figure 7.2. If the elemental spacing is $\lambda/2$, the butler matrix produces four beams. Although these beams overlap, they are mutually orthogonal. Surprisingly the Butler matrix was developed before the development of the FFT.

There are a number of drawbacks with multiple-beam formers, viz.

1. It is difficult to reconfigure the beam former. Most multiple beam formers can only produce fixed beams.
2. The separation between the multiple beams cannot be any less than that for orthogonal beams.
3. As the number of beams is increased, one has to keep track of the signal to noise ratio (SNR) of the individual beams.
4. As the array length becomes longer and the total span of the multiple beams increases, the difference between the arrival times of the wave-front from the source to the ends of the array become comparable to the inverse of the bandwidth of the signal used and the loss of SNR due to bandwidth effects becomes large.

Figure 7.2: A Blass beam forming networks (Panel (a)). Such a network requires $N^2$ phase shifters to form N beams from N antennas. On the other hand, the Butler beam forming network (Panels (b) and (c)) requires only $N\log(N)$ phase sifters to achieve the same result.