


Next: Further Reading
Up: Imaging With Dipolar Arrays
Previous: Square Kilometer Array (SKA)
Contents
An adaptive beam former is a device that is able to separate signals co-located
in the frequency band but separated in the spatial domain. This provides a means for
separating the desired signal from interfering signals. An adaptive beam former is
able to automatically optimise the array pattern by adjusting the elemental control
weights until a prescribed objective function is satisfied. An algorithm designed
for that purpose specifies the means by which the optimisation is achieved. These
devices use far more of the information available at the antenna aperture than
does a conventional beamformer.
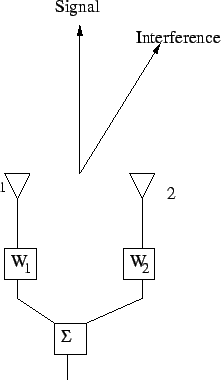
Figure 7.4:
A two element adaptive array for interference suppression. The array
simultaneously accepts a signal coming from the zenith, while rejecting
an interfering signal 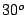 from the zenith by a suitable choice of
the weights
from the zenith by a suitable choice of
the weights 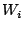 .
.
 |
The procedure used for steering and modifying an array's beam pattern in
order to enhance the reception of a desired signal, while simultaneously suppressing
interfering signals through complex weight selection is illustrated by the following
example. Let us consider the array shown in Figure 7.4. The array
consists of two antennas with a spacing of 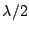 . Let the signal
. Let the signal 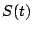 arriving
from a radio source at zenith is the desired signal. Let
arriving
from a radio source at zenith is the desired signal. Let 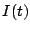 be an interfering
signal arriving from a direction
be an interfering
signal arriving from a direction
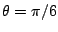 radians. The signal from each
element is multiplied by a variable complex weight
radians. The signal from each
element is multiplied by a variable complex weight 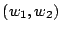 and the weighted
signals are then summed to form the array output. The array output due to the
desired signal is
and the weighted
signals are then summed to form the array output. The array output due to the
desired signal is
![\begin{displaymath}
Y(t) = A~e^{j2\pi ft} [w_1+w_2].
\end{displaymath}](img815.gif) |
(7.6.1) |
For the 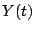 to be equal to
to be equal to 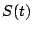 , it is necessary that
, it is necessary that
![\begin{displaymath}
RP [w_1] + RP [w_2] = 1
\end{displaymath}](img817.gif) |
(7.6.2) |
and
![\begin{displaymath}
IP [w_1] + IP [w_2] = 0.
\end{displaymath}](img818.gif) |
(7.6.3) |
Where RP and IP denote real and imaginary parts of the complex weights.
The interfering signal arrives at the element 2 with a phase lead of 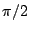 with
respect to the element 1. Consequently the array output due to the interfering
signal is given by
with
respect to the element 1. Consequently the array output due to the interfering
signal is given by
![\begin{displaymath}
Y_i(t) = [N e^{j2\pi ft}] w_1+[N e^{j2\pi ft + \pi/2}] w_2.
\end{displaymath}](img819.gif) |
(7.6.4) |
For the array response to the interference to be zero, it is necessary that
![\begin{displaymath}
RP [w_1] + RP [jw_2] = 0
\end{displaymath}](img820.gif) |
(7.6.5) |
and
![\begin{displaymath}
IP [w_2] + IP [jw_2] = 0.
\end{displaymath}](img821.gif) |
(7.6.6) |
The requirement that the array has to respond to only the radio source and not to
the interfering signal leads to the solution
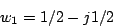 |
(7.6.7) |
and
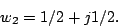 |
(7.6.8) |
With these weights, the array will accept the desired signal while simultaneously
rejecting the interference.
The method used in the above example exploits the fact that there is only one
directional interference source and uses the a priori information concerning the
frequency and the directions of both of the signals. A more practical processor should
not require such a detailed a priori information about the location, number and nature
of sources. But this example has demonstrated that a system consisting of an array,
which is configured with complex weights, provides numerous possibilities for
realising array system objectives. We need to only develop a practical processor for
carrying out the complex weight adjustment. In such a processor the choice of the
weighting will be based on the statistics of the signal of interest received at
the array. Basically the objective is to optimise the beamformer response with
respect to a prescribed criterion, so that the output contains minimal contribution
from the interfering signal.
There can be no doubt about the worsening observing situation in radio
astronomy due to the increased use of frequency space for communications. But a
pragmatic view is that it is hopeless to resist the increased use of frequency space
by others and we must learn to live with it. The saving grace is that the requirements
of mobile cellular, satellite and personal communication services systems are pushing
the advancement in technology to provide increasingly faster and less expensive digital
hardware. The present trend is to replace the analog functions of a radio receiver
with software or digital hardware. The ultimate goal is to directly digitise the RF
signal at the output of the receiving antenna and then implement the rest of the radio
functions in either digital hardware or software. Trends have evolved toward this goal
by incorporating digitisation closer and closer to the antenna at increasingly higher
frequencies and wider bandwidths. It is appropriate that the radio astronomer uses
this emerging technology to make the future radio telescopes interference free.
Adaptive arrays hold the key to this endeavour.



Next: Further Reading
Up: Imaging With Dipolar Arrays
Previous: Square Kilometer Array (SKA)
Contents
NCRA-TIFR


![]() . Let the signal
. Let the signal ![]() arriving
from a radio source at zenith is the desired signal. Let
arriving
from a radio source at zenith is the desired signal. Let ![]() be an interfering
signal arriving from a direction
be an interfering
signal arriving from a direction
![]() radians. The signal from each
element is multiplied by a variable complex weight
radians. The signal from each
element is multiplied by a variable complex weight ![]() and the weighted
signals are then summed to form the array output. The array output due to the
desired signal is
and the weighted
signals are then summed to form the array output. The array output due to the
desired signal is