Quantization

Figure 8.1: Transfer function of a two bit four level quantizer. The binary numbers corresponding to the quantized voltage range from 00 to 11. Quantization of a sine wave with such a quantizer is also shown.

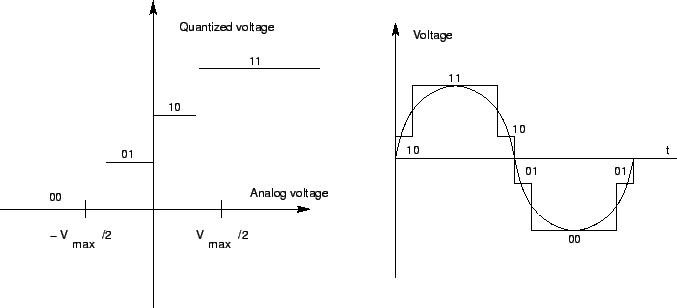
The amplitude of the sampled signal is a continuous value. Digital systems represent values using a finite number of bits. Hence the amplitude has to be approximated and expressed with these finite number of bits. This processes is called quantization. The quantized values are integer multiple of a quantity $q$ called the quantization step. An example of two bit (or equivalently four level) quantization is shown in Fig. 8.1. For the quantizer $q = V_{max}/2^2$, where $V_{max}$ is the maximum voltage (peak-to-peak) that can be expressed within an error of $\pm q/2$.

Figure 8.2: Power spectrum of band limited gaussian noise after one bit quantization. The spectrum of the original analog signal is shown with a solid line, while that of the quantized signal is shown with a dotted line.

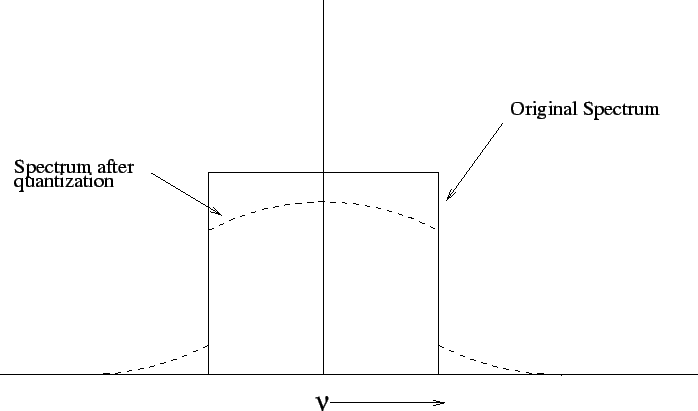Quantization distorts the sampled signal affecting both the amplitude and spectrum of the signal. This is evident from Fig. 8.1 for the case of a two bit four level quantized sine wave. The amplitude distortion can be expressed in terms of an error function $e(t) = s(t) - s_q(t)$, which is also called the quantization noise. Here $s_q(t)$ is the output of the quantizer. The variance of quantization noise under certain restricted conditions (such as uniform quantization) is $q^2/12$. The spectrum of quantization noise extends beyond the bandwidth $\Delta \nu$ of $s(t)$ (see Fig. 8.2). Sampling at the Nyquist rate ($2\Delta\nu$) therefore aliases the power of the quantization noise outside $\Delta \nu$ back into the spectral band of $s(t)$. For radio astronomy signals, the spectral density of the quantization noise within $\Delta \nu$ can be considered uniform and is $\sim$ $q^2/12\Delta\nu$ (assuming uniform quantization). Reduction in quantization noise is hence possible by oversampling $s(t)$ (i.e.  $f_s > 2\Delta\nu$) since it reduces the aliased power. For example, the signal to noise ratio of a digital measurement of the correlation function of s(t) (see Section 8.5) using a Nyquist sampling and a two bit four level quantizer is 88% of the signal to noise ratio obtained by doing analog correlation for Nyquist sampling and 94% if one were to sample at twice the Nyquist rate.

The largest value that can be expressed by a quantizer is determined by the number of bits ($M$) used for quantization. This value is $2^M-1$ for binary representation. The finite number of bits puts an upper bound on the amplitude of input voltage that can be expressed within an error $\pm q/2$. Signals with amplitude above the maximum value will be `clipped', thus producing further distortion. This distortion is minimum if the probability of amplitude of the signal exceeding $+V_{max}/2$ and $-V_{max}/2$ is less than $10^{-5}$. For a signal with a gaussian amplitude distribution this means that $V_{max} = 4.42\sigma$, $\sigma$ being the standard deviation of $s(t)$.