The inversion of the visibilities to make the Dirty Map is done
using FFT algorithm which requires that the function be sampled at
regular intervals and the number of samples be power of 2. For the
case of mapping the sky using an aperture synthesis telescope, this
implies that the visibility data be available on a regular 2D grid in
the ![]() plane. Thus re-gridding of the data onto a regular grid is
required by potentially interpolating the visibility to the grid
points, since the visibility function
plane. Thus re-gridding of the data onto a regular grid is
required by potentially interpolating the visibility to the grid
points, since the visibility function ![]() is measured at discrete
points
is measured at discrete
points ![]() which are not assured to be at regular intervals along
the
which are not assured to be at regular intervals along
the ![]() and
and ![]() axis.
axis.
Interpolation of ![]() is done by multiplying a function and
averaging all the measured points which lie within the range of the
function with a finite support base, centered at each grid point. The
resultant average value is assigned to the corresponding grid point.
This operation is equivalent to discrete convolution of
is done by multiplying a function and
averaging all the measured points which lie within the range of the
function with a finite support base, centered at each grid point. The
resultant average value is assigned to the corresponding grid point.
This operation is equivalent to discrete convolution of ![]() with the
above mentioned function and then sampling this convolution at the
grid points. The convolving function is referred to as the Gridding
Convolution Function (GCF). There are other ways of doing this
interpolation. However the interpolation in practice is done by
convolution since this results into predictable results in the map
plane which are easy to visualize. Also using GCF with finite support
base results into each grid point getting the value of the local
average of the visibilities.
with the
above mentioned function and then sampling this convolution at the
grid points. The convolving function is referred to as the Gridding
Convolution Function (GCF). There are other ways of doing this
interpolation. However the interpolation in practice is done by
convolution since this results into predictable results in the map
plane which are easy to visualize. Also using GCF with finite support
base results into each grid point getting the value of the local
average of the visibilities.
After gridding Eq. 11.2.5 becomes
The effect of gridding the visibilities on the map is to multiply the
map with function ![]() and since
and since ![]() has a finite support base (i.e. is
of finite extent),
has a finite support base (i.e. is
of finite extent), ![]() is infinite in extent which result into
aliasing in the map plane (the other cause of aliasing could be
under-sampling of the
is infinite in extent which result into
aliasing in the map plane (the other cause of aliasing could be
under-sampling of the ![]() -plane). The amplitude of the aliased
component from a position
-plane). The amplitude of the aliased
component from a position ![]() in the map is determined by
in the map is determined by
![]() . Ideally therefore, this function should be rectangular
function with the width equal to the size of the map and smoothly
going to zero immediately outside the map. However from the point of
efficiency of the gridding process, this is not possible, and GCF used
in practice have a trade-off between the roll-off properties at the
edge and flatness within the map.
. Ideally therefore, this function should be rectangular
function with the width equal to the size of the map and smoothly
going to zero immediately outside the map. However from the point of
efficiency of the gridding process, this is not possible, and GCF used
in practice have a trade-off between the roll-off properties at the
edge and flatness within the map.
Since the Dirty Map is multiplied by ![]() , if
, if ![]() is well known,
then effect of convolution by the GCF can be removed by point-wise
division of Dirty Map and Dirty Beam given by
is well known,
then effect of convolution by the GCF can be removed by point-wise
division of Dirty Map and Dirty Beam given by
![]() and
and ![]() for later processing, particularly in
deconvolution of
for later processing, particularly in
deconvolution of ![]() . In practice however, this division is not
carried out by evaluating
. In practice however, this division is not
carried out by evaluating ![]() over the map. Instead, for
efficiency purposes, this function is kept in the computer memory
tabulated with a resolution typically
over the map. Instead, for
efficiency purposes, this function is kept in the computer memory
tabulated with a resolution typically ![]() times the size of the
cell in the image.
times the size of the
cell in the image.
To take the Fourier transform of ![]() using the FFT algorithm one
needs to sample the right hand side of Eq. 11.3.6 by
multiplication with the re-sampling function
using the FFT algorithm one
needs to sample the right hand side of Eq. 11.3.6 by
multiplication with the re-sampling function ![]() given by
given by
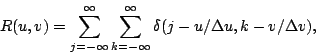 |
(11.3.7) |
![]() is usually real and even and is assumed to be separable as
is usually real and even and is assumed to be separable as
![]() . Various GCFs used in practice are listed
below. Functions listed below are in
1-dimension and are truncated (set to zero) for
. Various GCFs used in practice are listed
below. Functions listed below are in
1-dimension and are truncated (set to zero) for
![]() where
where ![]() is the size of the grid and
is the size of the grid and ![]() is the number of such
cells used.
is the number of such
cells used.
This amounts to simple averaging of all the ![]() -points with in the
rectangle defined by Eq. 11.3.9. However since its Fourier
transform is
-points with in the
rectangle defined by Eq. 11.3.9. However since its Fourier
transform is ![]() with large side lobes, it provides poor alias
rejection and is almost never used but is useful for intuitive
understanding.
with large side lobes, it provides poor alias
rejection and is almost never used but is useful for intuitive
understanding.
Typically ![]() ,
, ![]() and
and ![]() is used and
is used and ![]() can be expressed
in terms of error function.
can be expressed
in terms of error function.
For ![]() and
and ![]() , this is the normal
, this is the normal ![]() function expressed in
terms of
function expressed in
terms of ![]() function. As
function. As ![]() increases, the Fourier transform of this
function approaches a step function which is constant over the map and
zero outside.
increases, the Fourier transform of this
function approaches a step function which is constant over the map and
zero outside.
| (11.3.12) |
Of all the square integrable functions, this is the most optimal in
the sense that it has maximum contribution to the normalized area from
the part of ![]() which is with in the map. This is referred to as
the energy concentration ratio expressed as
which is with in the map. This is referred to as
the energy concentration ratio expressed as
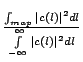 is maximized.
is maximized.