


Next: Mathematical details
Up: Signals in Radio Astronomy
Previous: Quasimonochromatic and Complex Signals
Contents
We have so far thought of the signal as a
function of time, after it enters the antenna. Let us now liberate
ourselves from one dimension (time) and think of the electric field as
existing in space and time, before it is collected by the antenna. In this
view, one can obtain a delayed version of the signal by moving along the
longitudinal direction (direction of the source). Thus, the frequency
content is obtained by Fourier transforming a longitudinal spatial
correlation. As explained in Chapter 2, the spatial
correlations transverse to the direction of propagation carry
information on the angular power spectrum of the signal, i.e. the energy
as a function of direction in the sky. With hindsight, this can be viewed
as a generalisation of the Wiener- Khinchin theorem to spatial
correlations of a complex electric field which is the sum of waves
propagating in many different directions. Historically, it arose quite
independently (and about at the same time!) in the context of optical
interference. This is the van Cittert-Zernike theorem of
Chapter 2.
Since one is now multiplying and averaging signals coming from different
antennas, this is called a ``cross correlation function''. To get a
non-vanishing average,
one needs to multiply 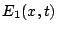 by
by 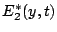 . The
complex conjugate sign in one of the terms ensures that this kind of
product looks at the phase difference. Writing out each signal as a
sum with random phases, the terms which leave a
non-zero average are the ones in which an
. The
complex conjugate sign in one of the terms ensures that this kind of
product looks at the phase difference. Writing out each signal as a
sum with random phases, the terms which leave a
non-zero average are the ones in which an
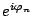 in an
in an 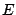 cancels a
cancels a
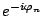 in an
in an 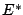 .
An
(ill-starred?) product of two complex
.
An
(ill-starred?) product of two complex
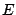 's with zero (or two!) complex conjugate signs would average to zero.
's with zero (or two!) complex conjugate signs would average to zero.



Next: Mathematical details
Up: Signals in Radio Astronomy
Previous: Quasimonochromatic and Complex Signals
Contents
NCRA-TIFR