Mathematical details

This section gives some more mathematical details of topics mentioned in the main text of the chapter.

We first give the generalisation of the two variable gaussian to the joint distribution of $k$ variables. Defining the covariance matrix $C_{ij}=\langle x_ix_j\rangle$, and $A=C^{-1}$, then we have

$$P(x_1\ldots x_k)=(2\pi)^{-k/2}(det~A)^{1/2} \exp\left(-\frac{1}{2}x^TAx\right)$$

The quadratic function $Q$ in the exponent has been written in matrix notation with $T$ for transpose. In full, it is $Q=\sum_{ij}{x_ia_{ij}x_j}$. Notice that the only information we need for the statistics of the amplitudes at $k$ different times is the autocorrelation function $C(\tau)$, evaluated at all time differences $t_i - t_j$. Formally this is stated as ``the gaussian process is defined by its second order statistics''.

What would be practically useful is an explicit formula for the average value of an arbitrary product $x_ix_jx_l \ldots$ in terms of the second order statistics $\langle x_1x_2\rangle \langle x_3x_7\rangle \ldots$ etc. The first step is to see that a product of an odd number of $x$'s averages to zero. (The contributions from $x_1 \ldots x_k$ & $-x_1 \ldots -x_k$ cancel).

For the case of an even number of gaussian variables to be multiplied and averaged, there is a standard trick to evaluate an integral like $\int{P(x_1\ldots x_k) x_3x_7 \ldots dx_1 \ldots}$. Define the Fourier transform of $P$,

$$G(k_1\ldots k_k)=\int\int {P(x_1\ldots x_k)e^{-ik_1x_1\ldots ik_kx_k}dx_1\ldots dx_k}$$

It is a standard result, derived by the usual device of completing the square, that this Fourier transform is itself a gaussian function of the $k$'s, given by

$$G(k_1,\ldots,k_k)= \exp\left(-\frac{1}{2}\sum_{ij}C_{ij}k_ik_j\right)\equiv \exp\left(-\frac{1}{2}k^TCk\right).$$

Differentiating with respect to $k_1$ and then $k_2$, and putting all $k$'s equal to zero, pulls down a factor $-x_1x_2$ into the integral and gives the desired average of $x_1x_2$. This trick now gives the average of the product of a string of $x$'s in the form of the ``pairing theorem''. This is easier to state by an example.

$$\langle x_1x_2x_3x_4\rangle = \langle x_1x_2\rangle \langle x... ...gle x_2x_4\rangle + \langle x_1x_4\rangle \langle x_2x_3\rangle$$

$$\equiv C_{12}C_{34}+C_{13}C_{24}+C_{14}C_{23}$$

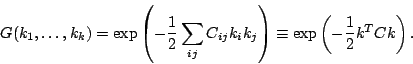
A sincere attempt to differentiate $G$ with respect to $k_1k_2k_3$ and $k_4$ and then put all $k$'s to zero will show that the $C$'s get pulled down in precisely this combination. Deeper thought shows that the pairing rule works even when the $x$'s are not all identical, i.e.,

$$\langle x^4\rangle = \langle x^2\rangle \langle x^2\rangle + ... ... x^2\rangle \langle x^2\rangle =3\langle x^2\rangle^2=3\sigma^4$$

or even $\langle x^{2n}\rangle = 1, 3, 5 \ldots (2n-1)\sigma^{2n}.$

The last property is easily checked from the single variable gaussian

$$(2\pi\sigma^2)^{-1/2}\exp(-x^2/2\sigma^2)$$

Since the pairing theorem allows one to calculate all averages, it could even be taken to define a gaussian signal, and that is what we do in the main text.

We now sketch a proof of the sampling theorem. Start with a band limited (i.e containing only frequencies less than $B$) signal sampled at the Nyquist rate, $E_r(n/2B)$. The following expression gives a way of constructing a continuous signal $E_c(t)$  from our samples.

$$E_c(t)=\sum_n E_r(n/2B) ~{\rm sinc}(2\pi B(t-\frac{n}{2B}))$$

It is also known as Whitaker's interpolation formula. Each sinc function is diabolically chosen to give unity at one sample point and zero at all the others, so $E_c(t)$ is guaranteed to agree with our samples of $E_r(t)$. It is also band limited (Fourier transform of a flat function extending from $-B$ to $+B$). All that is left to check is that it has the same Fourier coefficients as $E_r(t)$ (it does). And hence, we have reconstructed a band limited function from its Nyquist samples, as promised.

We add a few comments on the notion of Hilbert transform mentioned in the context of associating a complex signal with a real one. It looks rather innocent in the frequency domain, just subtract $\pi/2$ from the phase of each cosine in the Fourier series of $E_r(t)$ and reassemble to get $E_i(t)$. In terms of complex Fourier coefficients, it is a multiplication of the positive frequency component by $-i$ and of the corresponding negative frequency component by $+i$, Apart from the $i$, this is just multiplication by a step function of the symmetric type, jumping from minus 1 to plus 1 at zero frequency. Hence, in the time domain, it is a convolution of $E_r(t)$ by a kernel which is the Fourier transform of this step function, viz $1/t$ (the value t=0 being excluded by the usual principal value rule). Explicitly, we have

$$E_i(t)= \ \int E_r(s) P\left[ 1/(t-s)\right] ~ds/\pi$$

There is a similar formula relating $E_r$ to $E_i$ which only differs by a minus sign. This is sufficient to show that one needs values from the infinite past, and more disturbingly, future, of $t$ to compute $E_i(t)$. This is beyond the reach of ordinary mortals, even those equipped with the best filters and phase shifters. Practical schemes to derive the complex signal in real time thus have to make approximations as a concession to causality.

As remarked in the main text, there are many complex signals whose real parts would give our measured $E_r(t)$. The choice made above seemed natural because it was motivated by the quasimonochromatic case. It also has the mathematical property of creating a function which is very well behaved in the upper half plane of $t$ regarded as a complex variable, (should one ever want to go there). The reason is that $V(t)$ is constructed to have terms like $e^{i\omega t}$ with only positive values of $\omega$. Hence the pedantic name of ``analytic signal'' for this descendant of the humble phasor. It was the more general problem of continuing something given on the real axis to be well behaved in the upper half plane which attracted someone of Hilbert's IQ to this transform.