


Next: Polarization in Radio Astronomy
Up: Polarimetry
Previous: Polarimetry
Contents
Introduction
Consider the simplest kind of electromagnetic wave, i.e. a plane
monochromatic wave of frequency 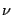 propagating along the +Z axis of
a cartesian co-ordinate system. Since electro-magnetic waves are transverse,
the electric field E must lie in the X-Y plane. Further since
the wave is mono-chromatic one can write
propagating along the +Z axis of
a cartesian co-ordinate system. Since electro-magnetic waves are transverse,
the electric field E must lie in the X-Y plane. Further since
the wave is mono-chromatic one can write
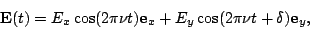 |
(15.1.1) |
i.e. the X and Y components of the electric field differ in phase by
a factor which does not depend on time. It can be shown15.1 that the implication of this is that over the course
of one period of oscillation, the tip of the electric field vector
in general traces out an ellipse. There are two special cases of
interest. The first is when 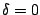 . In this case the tip
of the electric field vector traces out a line segment, and the wave
is said to be linearly polarized. The other special case is
when
. In this case the tip
of the electric field vector traces out a line segment, and the wave
is said to be linearly polarized. The other special case is
when 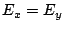 and
and
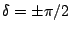 . In this case the electric
field vector traces out a circle in the X-Y plane, and depending on
the sense15.2 in which this circle is traversed the wave
is called either left circular polarized or right circular
polarized.
. In this case the electric
field vector traces out a circle in the X-Y plane, and depending on
the sense15.2 in which this circle is traversed the wave
is called either left circular polarized or right circular
polarized.
As you have already seen in chapter 1, signals in
radio astronomy are not monochromatic waves, but are better described
as quasi-monochromatic plane waves15.3. Further, the quantity that is typically
measured in radio astronomy is not related to the field (i.e. a voltage),
but rather a quantity that has units of voltage squared, i.e. related
to some correlation function of the field (see chapter 4).
For these reasons, it is usual to characterize the polarization properties
of the incoming radio signals using
quantities called Stokes parameters. Recall that for a
quasi monochromatic wave, the electric field E could be considered
to be the real part of a complex analytical signal
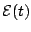 .
If the X and Y components of this complex analytical signal are
.
If the X and Y components of this complex analytical signal are
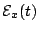 , and
, and
 , respectively, then
the four Stokes parameters are defined as:
, respectively, then
the four Stokes parameters are defined as:
 |
(15.1.2) |
where the angle brackets indicate taking the average value15.4.
The Stokes parameters as defined in equation (15.1.2) clearly depend
on the orientation of the co-ordinate system. In radio astronomy it
is conventional (see chapter 10) to take the +X axis to point
north and the +Y axis to point east. It is important to realize that
the Stokes parameters are descriptors of the intrinsic polarization
state of the electro-magnetic
wave, i.e. the Stokes vector  is a true vector. The
equations (15.1.2) simply give its components in a particular
co-ordinate system, the linear polarization co-ordinate system15.5. One would instead work in a circularly
polarized reference frame, i.e. where the electric field is decomposed
into two circularly
polarized components,
is a true vector. The
equations (15.1.2) simply give its components in a particular
co-ordinate system, the linear polarization co-ordinate system15.5. One would instead work in a circularly
polarized reference frame, i.e. where the electric field is decomposed
into two circularly
polarized components,
 , and
, and
 . The
relation between these components and the Stokes parameters are:
. The
relation between these components and the Stokes parameters are:
 |
(15.1.3) |
Interestingly, equations (15.1.3) are formally identical
to equations (15.1.2) apart from the following transformations
viz.
 ,
,
 ,
,
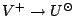 , where the superscript
, where the superscript  indicates
linear polarized co-ordinates and
indicates
linear polarized co-ordinates and  circular polarized co-ordinates.
Although these two co-ordinate systems are the ones most frequently used, the
Stokes vector could in principle be written in any co-ordinate system
based on two linearly independent (but not necessarily orthogonal)
polarization states. In fact, as we shall see, such non orthogonal
co-ordinate systems
will arise naturally when trying to describe measurements made with
non ideal radio telescopes.
circular polarized co-ordinates.
Although these two co-ordinate systems are the ones most frequently used, the
Stokes vector could in principle be written in any co-ordinate system
based on two linearly independent (but not necessarily orthogonal)
polarization states. In fact, as we shall see, such non orthogonal
co-ordinate systems
will arise naturally when trying to describe measurements made with
non ideal radio telescopes.
The degree of polarization of the wave is defined as
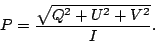 |
(15.1.4) |
From equation (15.1.2) we have
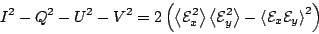 |
(15.1.5) |
and hence from the Schwarz inequality it follows that
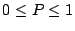 and that
and that 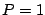 iff
iff
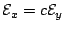 ,
where
,
where 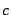 is some complex constant. For a mono-chromatic plane wave
(equation (15.1.1)) therefore,
is some complex constant. For a mono-chromatic plane wave
(equation (15.1.1)) therefore, 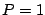 or equivalently
or equivalently
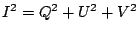 , i.e. there are only
three independent Stokes parameters. For a general quasi mono-chromatic
wave,
, i.e. there are only
three independent Stokes parameters. For a general quasi mono-chromatic
wave, 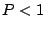 , and the wave is said to be partially polarized.
, and the wave is said to be partially polarized.
It is also instructive to examine the Stokes parameters separately for
the special case of a monochromatic plane wave. We have (see
equations (15.1.1) and (15.1.2)):
i.e. for a linearly polarized wave (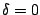 ) we have V = 0, and for
a circularly polarized wave (
) we have V = 0, and for
a circularly polarized wave (
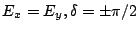 ) we have
) we have
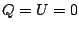 . So
. So 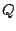 and
and 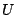 measure linear polarization, and
measure linear polarization, and 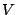 measures
circular polarization. This intepretation continues to be true
in the case of partially polarized waves.
measures
circular polarization. This intepretation continues to be true
in the case of partially polarized waves.
Footnotes
- ... shown15.1
- See
for example, Born & Wolf `Principles of Optics', Sixth Edition,
Section 1.4.2
- ... sense15.2
- Note that there is an additional ambiguity here,
i.e. are you looking along the direction of propagation of the wave,
or against it? To keep things interesting neither convention is
universally accepted, although in principle one should follow the
convention adopted by the IAU (Transactions of the IAU Vol. 15B,
(1973), 166.)
- ... waves15.3
- Recall that as all
astrophysically interesting sources are distant, the plane wave
approximation is a good one
- ... value15.4
- Strictly speaking this is the ensemble average. However, as always, we
will assume that the signals are ergodic, i.e. the ensemble average can
be replaced with the time average.
- ... system15.5
- These
polaraization co-ordinate systems are of course in some abstract polarization
space and not real space



Next: Polarization in Radio Astronomy
Up: Polarimetry
Previous: Polarimetry
Contents
NCRA-TIFR
![]() .
If the X and Y components of this complex analytical signal are
.
If the X and Y components of this complex analytical signal are
![]() , and
, and
![]() , respectively, then
the four Stokes parameters are defined as:
, respectively, then
the four Stokes parameters are defined as:
![]() ,
,
![]() ,
,
![]() , where the superscript
, where the superscript ![]() indicates
linear polarized co-ordinates and
indicates
linear polarized co-ordinates and ![]() circular polarized co-ordinates.
Although these two co-ordinate systems are the ones most frequently used, the
Stokes vector could in principle be written in any co-ordinate system
based on two linearly independent (but not necessarily orthogonal)
polarization states. In fact, as we shall see, such non orthogonal
co-ordinate systems
will arise naturally when trying to describe measurements made with
non ideal radio telescopes.
circular polarized co-ordinates.
Although these two co-ordinate systems are the ones most frequently used, the
Stokes vector could in principle be written in any co-ordinate system
based on two linearly independent (but not necessarily orthogonal)
polarization states. In fact, as we shall see, such non orthogonal
co-ordinate systems
will arise naturally when trying to describe measurements made with
non ideal radio telescopes.