


Next: Scintillation
Up: Ionospheric effects in Radio
Previous: Propagation Through an Inhomogeneous
Contents
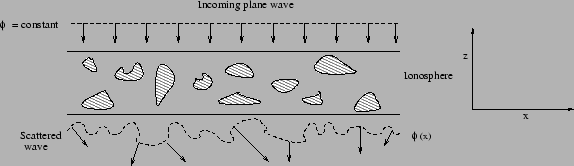
Figure 16.4:
Angular broadening.
 |
As discussed in the previous sections, the small scale fluctuations of
electron density in the
ionosphere lead to an excess phase for a radio wave passing through it.
This excess phase is given by
where 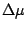 is the change in refractive index due to the
electron density fluctuation,
is the change in refractive index due to the
electron density fluctuation, 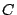 is a constant and
is a constant and 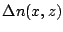 is
the fluctuation in electron density at the point (x,z) and the integral
is over the entire path traversed by the ray (see Figure 16.4).
is
the fluctuation in electron density at the point (x,z) and the integral
is over the entire path traversed by the ray (see Figure 16.4).
If we assume that 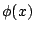 is a zero mean Gaussian random process,
with auto-correlation function given by
is a zero mean Gaussian random process,
with auto-correlation function given by
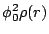 , where
, where
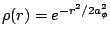 , then from the relation
above for
, then from the relation
above for 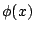 we can determine that
we can determine that
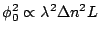 , where L is the total path length through the
ionosphere16.2. Let us
assume that a plane wavefront from an extremely distant point source is
incident on the top of such an ionosphere. In the absence of the ionosphere the
wave reaching the surface of the earth would also be a plane wave.
For a plane wave the correlation function of the electric field (i.e. the
visibility) is given by
, where L is the total path length through the
ionosphere16.2. Let us
assume that a plane wavefront from an extremely distant point source is
incident on the top of such an ionosphere. In the absence of the ionosphere the
wave reaching the surface of the earth would also be a plane wave.
For a plane wave the correlation function of the electric field (i.e. the
visibility) is given by
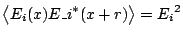 ,
i.e. a constant independent of
,
i.e. a constant independent of 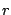 . On passage through the ionosphere
however, different parts of the wave front acquire different phases, and
hence the emergent wavefront is not plane. If
. On passage through the ionosphere
however, different parts of the wave front acquire different phases, and
hence the emergent wavefront is not plane. If 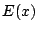 is the electric f
ield at some point on the emergent wave, then we have
is the electric f
ield at some point on the emergent wave, then we have
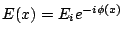 . Since
. Since 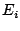 is just a constant, the correlation
function of the emergent electric field is
is just a constant, the correlation
function of the emergent electric field is
From our assumptions about the statistics of 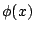 this can be
evaluated to give
this can be
evaluated to give
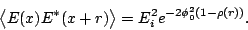 |
(16.5.6) |
If 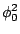 is very large, then the exponent is falls rapidly to zero
as
is very large, then the exponent is falls rapidly to zero
as 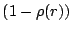 increases (or equivalently when
increases (or equivalently when 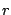 increases). It is
therefore adequate to evaluate it for small values of
increases). It is
therefore adequate to evaluate it for small values of 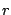 , for which
, for which  can be Taylor expanded to give
can be Taylor expanded to give
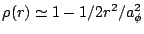 .
and we get
.
and we get
The emergent electric field hence has a finite coherence length
(while the coherence length of the incident plane wave was infinite).
From the van Cittert-Zernike theorem this is equivalent to saying
that the original unresolved point source has got blurred out to a
source of finite size. This blurring out of point sources is called
``angular broadening'' or ``scatter broadening''. If we define
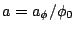 then the visibilities have a Gaussian distribution
given by
then the visibilities have a Gaussian distribution
given by
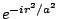 , meaning that the characteristic angular
size
, meaning that the characteristic angular
size 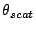 of the scatter broadened source is
of the scatter broadened source is
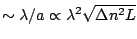 .
.
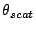 is called the ``scattering angle''.
is called the ``scattering angle''.
On the other hand if 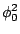 is small then the exponent
in eqn 16.5.6 can be Taylor expanded to give
is small then the exponent
in eqn 16.5.6 can be Taylor expanded to give
This corresponds to the visibilities from an unresolved core
(of flux density
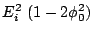 ) surrounded by a weak halo.
) surrounded by a weak halo.
Footnotes
- ...
ionosphere16.2
- This follows from the equation for
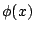 if you
also assume that
if you
also assume that
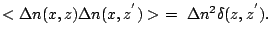

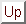


Next: Scintillation
Up: Ionospheric effects in Radio
Previous: Propagation Through an Inhomogeneous
Contents
NCRA-TIFR

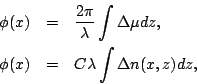
![]() is a zero mean Gaussian random process,
with auto-correlation function given by
is a zero mean Gaussian random process,
with auto-correlation function given by
![]() , where
, where
![]() , then from the relation
above for
, then from the relation
above for ![]() we can determine that
we can determine that
![]() , where L is the total path length through the
ionosphere16.2. Let us
assume that a plane wavefront from an extremely distant point source is
incident on the top of such an ionosphere. In the absence of the ionosphere the
wave reaching the surface of the earth would also be a plane wave.
For a plane wave the correlation function of the electric field (i.e. the
visibility) is given by
, where L is the total path length through the
ionosphere16.2. Let us
assume that a plane wavefront from an extremely distant point source is
incident on the top of such an ionosphere. In the absence of the ionosphere the
wave reaching the surface of the earth would also be a plane wave.
For a plane wave the correlation function of the electric field (i.e. the
visibility) is given by
![]() ,
i.e. a constant independent of
,
i.e. a constant independent of ![]() . On passage through the ionosphere
however, different parts of the wave front acquire different phases, and
hence the emergent wavefront is not plane. If
. On passage through the ionosphere
however, different parts of the wave front acquire different phases, and
hence the emergent wavefront is not plane. If ![]() is the electric f
ield at some point on the emergent wave, then we have
is the electric f
ield at some point on the emergent wave, then we have
![]() . Since
. Since ![]() is just a constant, the correlation
function of the emergent electric field is
is just a constant, the correlation
function of the emergent electric field is
![]() is small then the exponent
in eqn 16.5.6 can be Taylor expanded to give
is small then the exponent
in eqn 16.5.6 can be Taylor expanded to give
![\begin{eqnarray*}
\bigl<E(x)E^*(x+r)\bigr> &=& E_i^2 \bigl[1 - 2\phi_0^2(1-\rho(...
...1 - 2\phi_0^2) + 2\phi_0^2
e^{-r^2\over 2 a_\phi^2} \bigr]. \\
\end{eqnarray*}](img1398.gif)