


Next: Further Reading
Up: GMRT Antennas and Feeds
Previous: 1000-1450 MHz Feed
Contents
GMRT Antenna Efficiencies
The efficiency relations shown in Section 19.5,
have not considered the effect of aperture blockage by feeds and feed-support
frames (``quadripod legs'' in GMRT-parlance). Simple geometrical
optics based models for such computation exist,[16] which are used along
with GMRT-specific efficiency relations, to produce the following table.
Limitations of this model are highlighted in [17].
Some of the loss terms can be expressed as equivalent noise
temperatures (see Chapter 3). The spillover temperature
is given by (see also Eqn 19.4.14)
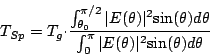 |
(19.8.24) |
where 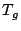 is the ground temperature. Considering the reflectance
of soil at microwave frequencies, it is presumed as
is the ground temperature. Considering the reflectance
of soil at microwave frequencies, it is presumed as 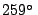 K.
K.
Similarly, the mesh-leakage 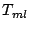 , scattered radiation by
the feed- support frames
, scattered radiation by
the feed- support frames 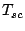 , can also be expressed in terms of
, can also be expressed in terms of
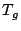 . The overall system temperature (see Chapter 3) is the sum
of all these and the receiver noise temperature,
. The overall system temperature (see Chapter 3) is the sum
of all these and the receiver noise temperature, 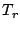 and the sky
temperature,
and the sky
temperature,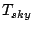 , which is assumed to be,
, which is assumed to be,
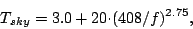 |
(19.8.25) |
where 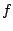 is the frequency of the received signal (in MHz). Hence
is the frequency of the received signal (in MHz). Hence
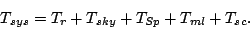 |
(19.8.26) |
Finally the figure-of-merit of any radio antenna, is the
gain-by-system temperature ratio, 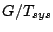 , expressed as :
, expressed as :
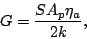 |
(19.8.27) |
where 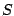 is flux density in units of Jansky,
is flux density in units of Jansky, 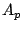 , is the physical
area of the parabolic dish and
, is the physical
area of the parabolic dish and 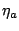 is the overall aperture
efficiency.
For a 1 Jy. source at the beam of the antenna and value of Boltzmann's
constant
is the overall aperture
efficiency.
For a 1 Jy. source at the beam of the antenna and value of Boltzmann's
constant 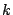 included in the above relation,
included in the above relation,
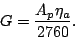 |
(19.8.28) |
Hence, the ratio 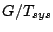 is expressed in units of
is expressed in units of 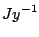 .
.
A summary of the relevant parameters for the GMRT antennas
is given in Table 19.4. These have been computed based
on the following assumptions.
-
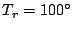 K for 150,233 and 327 MHz bands;
K for 150,233 and 327 MHz bands;
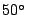 K for 610 MHz and
K for 610 MHz and 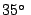 K for the 1000 to
1400 MHz bands.
K for the 1000 to
1400 MHz bands.
- The surface rms,
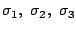 values are
8.0, 9.0, and 14.0 mm respectively.
values are
8.0, 9.0, and 14.0 mm respectively.
The agreement between the observed HPBW, gain and system temperature
and the computed values is in general quite good.
Table 19.4:
Calculated aperture efficiencies and system temperatures for the GMRT
antennas.
| |
Frequency (MHz) |
| Eff. |
150 |
233 |
327 |
610 |
1000 |
1200 |
1400 |
| Tap Eff. |
0.689 |
0.823 |
0.715 |
0.775 |
0.566 |
0.533 |
0.592 |
| Spill. Eff. |
0.952 |
0.799 |
0.944 |
0.835 |
0.967 |
0.971 |
0.971 |
| Mesh Eff. |
0.999 |
0.999 |
0.998 |
0.991 |
0.943 |
0.941 |
0.94 |
| RMS Eff. |
0.997 |
0.992 |
0.986 |
0.948 |
0.88 |
0.835 |
0.78 |
| Aper. Eff. |
0.652 |
0.651 |
0.664 |
0.608 |
0.452 |
0.405 |
0.422 |
Tsys( K) K) |
428 |
229 |
152 |
92 |
65 |
77 |
62 |
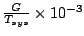 |
0.877 |
1.64 |
2.53 |
3.81 |
4.04 |
3.02 |
3.17 |
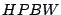 |
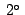 52'39'' 52'39'' |
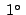 51'06'' 51'06'' |
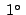 21'15'' 21'15'' |
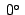 42'48'' 42'48'' |
|
 19'26'' 19'26'' |
|
|



Next: Further Reading
Up: GMRT Antennas and Feeds
Previous: 1000-1450 MHz Feed
Contents
NCRA-TIFR
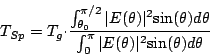
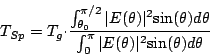
![]() , scattered radiation by
the feed- support frames
, scattered radiation by
the feed- support frames ![]() , can also be expressed in terms of
, can also be expressed in terms of
![]() . The overall system temperature (see Chapter 3) is the sum
of all these and the receiver noise temperature,
. The overall system temperature (see Chapter 3) is the sum
of all these and the receiver noise temperature, ![]() and the sky
temperature,
and the sky
temperature,![]() , which is assumed to be,
, which is assumed to be,