Antenna Patterns

The most important characteristic of an antenna is its ability to absorb radio waves incident upon it. This is usually described in terms of its effective aperture. The effective aperture of an antenna is defined as

$$A_e = {{\rm Power ~density ~available~at~the~antenna~terminal... ...over ~{\rm Flux~density~of~the~wave~incident~on~the~antenna}}$$

The units are

$${ W/Hz \over W/m^2/Hz } = m^2$$

The effective area is a function of the direction of the incident wave, because the antenna works better in some directions than in others. Hence

$$A_e~~ =~~A_e(\theta, \phi)$$

This directional property of the antenna is often described in the form of a power pattern. The power pattern is simply the effective area normalized to be unity at the maximum, i.e.

$$P(\theta,\phi)~~=~~ {A_e(\theta, \phi) \over A_e^{max}}$$

The other common way to specify the directive property of an antenna is the field pattern. Consider an antenna receiving radio waves from a distant point source. The voltage at the terminals of the antenna as a function of the direction to the point source, normalized to unity at maximum, is called the field pattern $f(\theta,\phi)$ of the antenna. The pattern of an antenna is the same regardless of whether it is used as a transmitting antenna or as a receiving antenna, i.e. if it transmits efficiently in some direction, it will also receive efficiently in that direction. This is called Reciprocity, (or occassionaly Lorentz Reciprocity) and follows from Maxwell's equations. From reciprocity it follows that the electric field far from a transmitting antenna, normalized to unity at maximum, is simply the Field pattern $f(\theta,\phi)$. Since the power flow is proportional to the square of the electric field, the power pattern is the square of the field pattern. The power pattern is hence real and positive semi-definite.

Figure 3.9: Schematic power pattern of an antenna

A typical power pattern is shown in Figure 3.9. The power pattern has a primary maximum, called the main lobe and several subsidiary maxima, called side lobes. The points at which the main lobe falls to half its central value are called the Half Power points and the angular distance between these points is called the Half Power Beamwidth (HPBW). The minima of the power pattern are called nulls. For radio astronomical applications one generally wants the HPBW to be small (so that the nearby sources are not confused with one another), and the sidelobes to be low (to minimize stray radiation). From simple diffraction theory it can be shown that the HPBW of a reflecting telescope is given by

$$\Theta_{HPBW} \sim \lambda/D$$

where D is the physical dimension of the telescope. $\lambda$ and D must be measured in the same units and $\Theta$ is in radians. So the larger the telescope, the better the resolution. For example, the HPBW of a 700 foot telescope at 2380 MHz is about 2 arcmin. This is very poor resolution - an optical telescope ( $\lambda \sim 5000 \AA$), a few inches in diameter has a resolution of a few arc seconds. However, the resolution of single dish radio telescopes, unlike optical telescopes, is not limited by atmospheric turbulence. Figure 3.10 shows the power pattern of the (pre-upgrade) Arecibo telescope at 2380 MHz. Although the telescope is 1000 ft in diameter, only a 700 ft diameter aperture is used at any given time, and the HPBW is about 2 arc min. There are two sidelobe rings, which are not quite azimuthally symmetric.

Figure 3.10: The (pre-upgrade) Arecibo power pattern at 2380 MHz. The HPBW is $\sim 2^{'}$.

There are two other patterns which are sometimes used to describe antennas. The first is the directivity $D(\theta,\phi)$. The directivity is defined as:

$$D(\theta,\phi) = {{\rm Power~emitted~into}~ (\theta,\phi) \over ({\rm Total~power~emitted})/4 \pi}$$ (3.4.1)

$$= {4 \pi P(\theta,\phi) \over \int P(\theta,\phi)~d\Omega }$$ (3.4.2)

This is the `transmitting' pattern of the antenna, and from reciprocity should be the same as the recieving power pattern to within a constant factor. We will shortly work out the value of this constant. The other pattern is the gain $G(\theta,\phi)$. The gain is defined as:

$$G(\theta,\phi) = {{\rm Power~emitted~into}~ (\theta,\phi) \over ({\rm Total~power~input})/4 \pi}$$ (3.4.3)

The gain is the same as the directivity, except for an efficiency factor. Finally a figure of merit for reflector antennas is the aperture efficiency, $\eta$. The aperture efficiency is defined as:

$$\eta = {A_{e}^{max} \over A_g}$$ (3.4.4)

where $A_g$ is the geometric cross-sectional area of the main reflector. As we shall prove below, the aperture efficiency is at most 1.0.

Figure 3.11: The antenna temperature is the convolution of the sky brightness and the telescope beam.

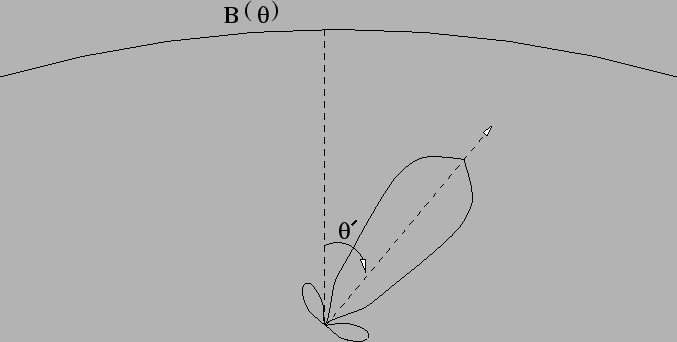Consider observing a sky brightness distribution $B(\theta)$ with a telescope with a power pattern like that shown in Figure 3.9. The power available at the antenna terminals is the integral of the brightness in a given direction times the effective area in that direction (Figure 3.11).

$$W(\theta^{'} ) = {1 \over 2 }\int B(\theta) A_{e}(\theta -\theta^{'} ) d\theta$$ (3.4.5)

where the available power $W$ is a function of $\theta^{'}$, the direction in which the telescope is pointed. The factor of ${1 \over 2}$ is to account for the fact that only one polarization is absorbed by the antenna. In two dimensions, the expression for $W$ is:

$$W(\theta^{'} ,\phi^{'} ) = {1 \over 2} \int B(\theta,\phi) A... ...heta-\theta^{'} , \phi - \phi^{'} ) \sin(\theta)d\theta d\phi$$ (3.4.6)

in temperature units, this becomes:

$$T_A(\theta^{'} ,\phi^{'} ) = {1 \over 2} \int {T_B(\theta,\p... ...\theta-\theta^{'} ,\phi - \phi^{'} ) \sin(\theta)d\theta d\phi$$ (3.4.7)

or

$$T_A(\theta^{'} ,\phi^{'} ) = {A_e^{max} \over \lambda^2} \in... ...\theta-\theta^{'} ,\phi - \phi^{'} ) \sin(\theta)d\theta d\phi$$ (3.4.8)

So the antenna temperature is a weighted average of the sky temperature, the weighting function being the power pattern of the antenna. Only if the power pattern is a single infinitely sharp spike is the antenna temperature the same as the sky temperature. For all real telescopes, however, the antenna temperature is a smoothed version of the sky temperature. Supposing that you are making a sky survey for sources. Then a large increase in the antenna temperature could mean either that there is a source in the main beam, or that a collection of faint sources have combined to give a large total power. From the statistics of the distribution of sources in the sky (presuming you know it) and the power pattern, one could compute the probability of the latter event. This gives a lower limit to the weakest detectable source, below this limit,(called the confusion limit), one can no longer be confident that increases in the antenna temperature correspond to a single source in the main beam. The confusion limit is an important parameter of any given telescope, it is a function of the frequency and the assumed distribution of sources.

Now consider an antenna terminated in a resistor, with the entire system being placed in a black box at temperature $T$. After thermal equilibrium has been reached, the power flowing from the resistor to the antenna is:

$$P_{R \rightarrow A} = kT$$

The power flow from the antenna to the resistor is (from equation (3.4.9) and using the fact that the sky temperature is the same everywhere)

$$P_{A \rightarrow R}= \bigl( {A_e^{max}kT \over \lambda^2} \bigr) \int P(\theta,\phi) d \Omega$$

In thermal equilibrium the net power flow has to be zero, hence

$$A_e^{max} = {\lambda^2 \over \int P(\theta,\phi) d\Omega},$$ (3.4.9)

i.e. the maximum effective aperture is determined by the shape of the power pattern alone. The narrower the power pattern the higher the aperture efficiency. For a reflecting telescope,

$$\int P(\theta,\phi)d \Omega \sim \Theta_{HPBW}^2 \sim \bigl( {\lambda \over D} \bigr)^2.$$

so

$$A_e^{max} \sim D^2.$$

The max. effective aperture scales like the geometric area of the reflector, as expected. Also from equation 3.4.10

$$A_{e} = A_e^{max} P(\theta,\phi) = {\lambda^2 P(\theta, \phi) \over \int P(\theta,\phi) d \Omega}.$$ (3.4.10)

Comparing this with equation (3.4.1) gives the constant that relates the effective area to the directivity

$$D(\theta,\phi) = {4 \pi \over \lambda^2} A_{e}(\theta,\phi).$$ (3.4.11)

As an application for all these formulae, consider the standard communications problem of sending information from antenna 1 (gain $G_1 (\theta,\phi)$, input power $P_1$) to antenna 2 (directivity $D_2(\theta^{'} ,\phi^{'} )$), at distance R away. What is the power available at the terminals of antenna 2?

The flux density at antenna 2 is given by:

$$S = {P_1 \over 4 \pi R^2} G_1(\theta,\phi)$$

. i.e., the power falls off like $R^2$, but is not isotropically distributed. (The gain $G_1$ tells you how collimated the emission from antenna 1 is). The power available at the terminals of antenna 2 is:

$$W = A_{2e} S = {P_1 \over 4 \pi R^2} G_1(\theta,\phi) A_{2e}$$

substituting for the effective aperture from equation (3.4.12)

$$W = \bigl( {\lambda \over 4 \pi R }\bigr)^2 P_1 G_1(\theta, \phi) D_2(\theta^{'} ,\phi^{'} )$$

This is called the Friis transmission equation. In Radar astronomy, there is a very similar expression for the power available at an antenna after bouncing off an unresolved target (the radar range equation). The major difference is that the signal has to make a round trip, (and the target reradiates power falling on it isotropically), so the received power falls like the fourth power of the distance to the target.