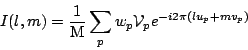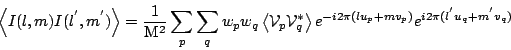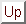


Next: Calibration
Up: Sensitivity and Calibration for
Previous: Sensitivity and Calibration for
Contents
As we discussed earlier, an aperture synthesis telescope
can be regarded as a collection of two element interferometers.
Hence, for understanding the sensitivity of such a telescope, it
is easier to first start with the case of a two element interferometer.
Consider such an interferometer composed of two antennas 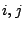 , (of
identical gains, but possibly different system temperatures), looking
at a point source of flux density S. We assume that the point source is at the
phase center5.1and hence that in the absence of noise the visibility phase is zero.
Let the individual antenna gains5.2be G and system temperatures be T
, (of
identical gains, but possibly different system temperatures), looking
at a point source of flux density S. We assume that the point source is at the
phase center5.1and hence that in the absence of noise the visibility phase is zero.
Let the individual antenna gains5.2be G and system temperatures be T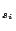 and T
and T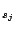 . If
. If
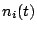 and
and 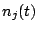 are the noise voltages of antennas
are the noise voltages of antennas 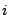 and
and 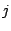 respectively,then
respectively,then
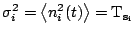 , and
, and
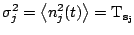 . Similarly if
. Similarly if 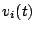 and
and
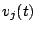 are the voltages induced by the incoming radiation from
the point source,
are the voltages induced by the incoming radiation from
the point source,
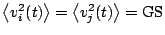 . The
instantaneous correlator5.3 output is given by:
. The
instantaneous correlator5.3 output is given by:
The mean5.4 of the correlator output is hence:
where we have assumed that the noise voltages of the two antennas
are not correlated, and also of course that the signal voltages are
not correlated with the noise voltages. 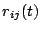 is hence an unbiased
estimator of the true visibility.
is hence an unbiased
estimator of the true visibility.
To determine the noise in the correlator output, we would need
to compute the rms of 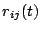 for which we need to be able to
work out:
for which we need to be able to
work out:
where for ease of notation we have stopped explicitly specifying that
all voltages are functions of time. This quantity is not trivial to
work out in general. However, if we assume that all the random processes
involved are Gaussian
processes5.5 the complexity is considerably reduced because for Gaussian
random variables the fourth moment can then be expressed in terms of
products of the second moment. In particular5.6, if
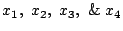 have a
joint gaussian distribution then:
have a
joint gaussian distribution then:
Rather than directly computing
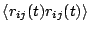 ,
it is instructive first to consider the more general quantity
,
it is instructive first to consider the more general quantity
viz. the cross-correlation between the outputs of interferometers 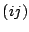 and
and 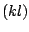 . We have:
. We have:
The case we are currently interested in is
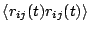 ,
which from eqn(5.1.3) is:
,
which from eqn(5.1.3) is:
To get the variance of 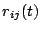 we need to subtract the square
of the mean of
we need to subtract the square
of the mean of 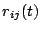 from the expression in eqn(5.1.4).
Substituting for
from the expression in eqn(5.1.4).
Substituting for
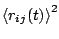 from eqn(5.1.1)
we have:
from eqn(5.1.1)
we have:
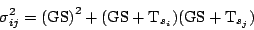 |
(5.1.5) |
Note that the angular brackets denote ensemble averaging. In real
life of course one cannot do an ensemble average. Instead
one does an average over time, i.e. we work in terms of a time averaged
correlator output
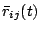 , defined as
, defined as
As can easily be verified,
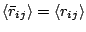 .
However, computing the second moment, viz.,
.
However, computing the second moment, viz.,
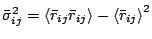 is slightly more tricky. It can be
shown5.7 that if
is slightly more tricky. It can be
shown5.7 that if 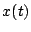 is a zero mean stationary process and that
is a zero mean stationary process and that 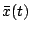 is the time average
of
is the time average
of 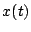 over the interval
over the interval
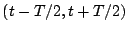 , then
, then
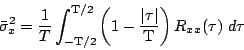 |
(5.1.6) |
where 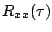 is the auto-correlation function of
is the auto-correlation function of 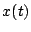 ,
and
,
and 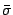 is the variance of
is the variance of 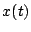 . Now,
if
. Now,
if 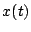 is a quasi-sinusoidal process with bandwidth
is a quasi-sinusoidal process with bandwidth 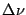 ,
then the integral of
,
then the integral of 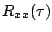 will be negligible outside
the coherence time
will be negligible outside
the coherence time 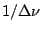 . Further, if
. Further, if
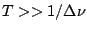 ,
then the factor in parenthesis in eqn(5.1.6) can be
taken to be
,
then the factor in parenthesis in eqn(5.1.6) can be
taken to be 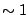 for
for
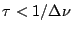 . Hence we have:
. Hence we have:
where
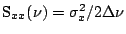 is the power
spectrum5.8 of
is the power
spectrum5.8 of 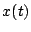 . From eqn(5.1.7)
and eqn(5.1.5) we hence have
. From eqn(5.1.7)
and eqn(5.1.5) we hence have
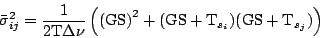 |
(5.1.8) |
Putting all this together we get that the signal to noise ratio of a two
element interferometer is given by:
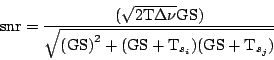 |
(5.1.9) |
There are two special cases which often arise in practice. The
first is when the source is weak, i.e.
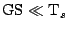 . In this
case the snr becomes
. In this
case the snr becomes
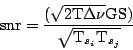 |
(5.1.10) |
For a single dish with the collecting area equal to the sum
of the collecting areas of antennas  and
and 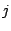 (i.e. with gain
(i.e. with gain 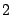 G),
and with system temperature
G),
and with system temperature
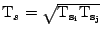 the
signal to noise would have been a factor of
the
signal to noise would have been a factor of 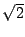 better5.9. The
loss of signal to noise in the two element interferometer is because
one does not measure the auto-correlations of antennas
better5.9. The
loss of signal to noise in the two element interferometer is because
one does not measure the auto-correlations of antennas 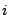 and
and 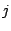 .
Only their cross-correlation has been measured. In a sigle
dish one would have effectively measured the cross-correlation
as well as the auto-correlations.
.
Only their cross-correlation has been measured. In a sigle
dish one would have effectively measured the cross-correlation
as well as the auto-correlations.
The other special case of interest is when the source is extremely
bright, i.e.
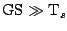 . In this case, the signal to
noise ratio is:
. In this case, the signal to
noise ratio is:
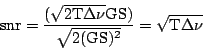 |
(5.1.11) |
This is as expected, because for very bright sources, one is limited by
the Poisson fluctuations of the source brightness, and hence one would
expect the signal to noise ratio to go as the square root of the number
of independent measurements. Since one gets an independent measurement
every 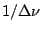 seconds, the total number of independent measurements
in a time T is just T
seconds, the total number of independent measurements
in a time T is just T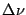 .
.
Having derived the signal to noise ratio for a two element interferometer,
let us now consider the case of an N element interferometer. This can
be considered as 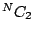 two element interferometers. Let us take
the case where the source is weak. Then from eqn(5.1.3) the
correlation between
two element interferometers. Let us take
the case where the source is weak. Then from eqn(5.1.3) the
correlation between 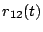 and
and 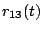 is given by
is given by
The outputs are uncorrelated, even though these two interferometers
have one antenna in common5.10. Similarly, one can show that (as expected) the outputs
of two two-element interferometers with no antenna in common are uncorrelated.
Since the 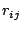 's are all uncorrelated with one another,
the rms noise can simply be added in quadrature. In particular, for
an N element array, where all the antennas are identical and have
the same system temperature, the signal to noise ratio while looking
at a weak source is:
's are all uncorrelated with one another,
the rms noise can simply be added in quadrature. In particular, for
an N element array, where all the antennas are identical and have
the same system temperature, the signal to noise ratio while looking
at a weak source is:
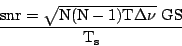 |
(5.1.13) |
This is the fundamental equation5.11
that is used to estimate the integration time required for a given
observation. The signal to noise ratio for an N element interferometer
is less than what would have been expected for a single dish telescope
with area N times that of a single element of the interferometer, but
only by the factor N/
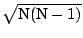 . The lower sensitivity is again
because the N auto-correlations have not been measured. For large
N however, this loss of information is negligible. For the GMRT, N
. The lower sensitivity is again
because the N auto-correlations have not been measured. For large
N however, this loss of information is negligible. For the GMRT, N 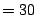 and
N/
and
N/
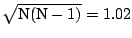 , hence the snr is essentially the same as
that of a single dish with 30 times the collecting area of a single
GMRT dish.
, hence the snr is essentially the same as
that of a single dish with 30 times the collecting area of a single
GMRT dish.
For a complex correlator5.12, the analysis that we have just done holds
separately for the cosine and sine channels of the correlator. If we
call the outputs of such a correlator 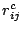 and
and 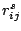 then
it can be shown that the noise in
then
it can be shown that the noise in 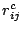 and
and 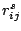 is
uncorrelated. Further
since the time averaging can be regarded as the adding together of a
large number of independent samples (
is
uncorrelated. Further
since the time averaging can be regarded as the adding together of a
large number of independent samples (
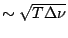 ),
from the central limit theorem, the statistics of the noise in
),
from the central limit theorem, the statistics of the noise in
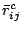 and
and
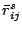 are well approximated as
Gaussian. It is then possible to derive the statistics of functions
of
are well approximated as
Gaussian. It is then possible to derive the statistics of functions
of
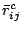 and
and
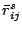 , such as the visibility
amplitude (
, such as the visibility
amplitude (
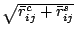 ) and the visibility
phase (
) and the visibility
phase (
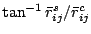 ). For example, it
can be shown that the visibility amplitude has a Rice
distribution5.13
). For example, it
can be shown that the visibility amplitude has a Rice
distribution5.13
For an extended source, the entire analysis that we have
done continues to hold, with the exception that S should be treated
as the correlated part of the source flux density. For example, at low
frequencies, the Galactic background is often much larger than the
receiver noise and one would imagine that the limiting case of large
source flux density (i.e. eqn(5.1.11) is applicable. However,
since this background is largely resolved out at even modest spacings,
its only effect is an increase in the system temperature.
Finally we look at the noise in the image plane, i.e.
after Fourier transformation of the visibilities. Since most of
the astronomical analysis and interpretation will be based on
the image, it is the statistics in the image plane that is usually
of interest. The intensity at some point 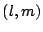 in the image
plane is given by:
in the image
plane is given by:
where 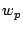 is the weight5.14
given to the
is the weight5.14
given to the 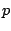 th visibility measurement
th visibility measurement 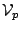 , and there are
a total of M independent measurements. The cross-correlation function
in the image plane,
, and there are
a total of M independent measurements. The cross-correlation function
in the image plane,
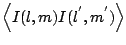 is hence:
is hence:
In the absence of any sources, the visibilities are uncorrelated with
one another, and hence, we have
Hence in the case that all the noise on each measurement is the same, and
that the weights given to each visibility point is also the same, (i.e.
uniform tapering), the correlation in the map plane has exactly the same
shape as the dirty beam. Further the variance in image plane would then
be
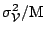 , where
, where
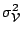 is the
noise on a single visibility measurement. This is equivalent to
eqn(5.1.13), as indeed it should be.
is the
noise on a single visibility measurement. This is equivalent to
eqn(5.1.13), as indeed it should be.
Because the noise in the image plane has a correlation function
shaped like the dirty beam, one can roughly take that the noise in
each resolution element is uncorrelated. The expected statistics after
simple image plane operations (like smoothing) can hence be worked out.
However, after more complicated operations, like the various possible
deconvolution operations, the statistics in the image plane are not
easy to derive.
Footnotes
- ... center5.1
- See Chapter 4.
- ... gains5.2
- Here the gain is taken to
be in units of Kelvin per Jansky of flux in the matched polarization
- ... correlator5.3
- Here we are dealing with an ordinary
correlator, not the complex correlator introduced in the chapter
on two element interferometers.
- ... mean5.4
- Note that the average being taken over here
is ensemble average, and not an average over
time.
- ...
processes5.5
- Recall from the discussion of sensitivity of a
single dish telescope that the central limit theorem ensures that
the signal and noise statistics will be well approximated by a Gaussian.
This of course does not include `systematics', like eg. interference,
or correlator offsets because of bit getting stuck in the on or off mode
etc.
- ... particular5.6
- The derivation
of this expression is particularly straightforward if one works with
the moment generating function; see also the derivation sketched in
Chapter 1.
- ...
shown5.7
- Papoulis, `Probability, Random Variables &
Stochastic Processes', Third Edition, Chapter 10
- ...
spectrum5.8
- Where we have made the additional assumption that
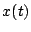 is a white noise process, i.e. that its spectrum is flat.
The power spectrum for such processes is easily derived from noting
that
is a white noise process, i.e. that its spectrum is flat.
The power spectrum for such processes is easily derived from noting
that
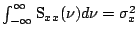 , and
that for a quasi-sinosoidal proccess of bandwidth
, and
that for a quasi-sinosoidal proccess of bandwidth 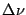 , the
integrand is non zero only over an interval
, the
integrand is non zero only over an interval 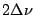 (including
the negative frequencies).
(including
the negative frequencies).
- ... better5.9
- As
you can easily derive from eqns 5.1.1 and 5.1.3 by
putting
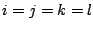 . Note that in this case eqn 5.1.1 becomes
. Note that in this case eqn 5.1.1 becomes
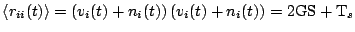
- ... common5.10
- This may seem counter intuitive,
but note that the outputs are only uncorrelated, they are not
independent.
- ... equation5.11
- In some references, an efficiency
factor
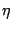 is introduced to account for degradation of signal to noise
ratio because of the noise introduced by finite precision digital
correlation etc. This factor has been ignored here, or equivalently
one can assume that it has been absorbed into the system temperature.
is introduced to account for degradation of signal to noise
ratio because of the noise introduced by finite precision digital
correlation etc. This factor has been ignored here, or equivalently
one can assume that it has been absorbed into the system temperature.
- ... correlator5.12
- See the chapter on two element
interferometers
- ...
distribution5.13
- Papoulis, `Probability, Random Variables
& Stochastic Processes', Third Edition, Chapter 6.
- ... weight5.14
- As discussed in Chapter 11,
this weight is in general a combination of weights chosen from signal to noise
ratio considerations and from synthesized beam shaping considerations.



Next: Calibration
Up: Sensitivity and Calibration for
Previous: Sensitivity and Calibration for
Contents
NCRA-TIFR
![]() , (of
identical gains, but possibly different system temperatures), looking
at a point source of flux density S. We assume that the point source is at the
phase center5.1and hence that in the absence of noise the visibility phase is zero.
Let the individual antenna gains5.2be G and system temperatures be T
, (of
identical gains, but possibly different system temperatures), looking
at a point source of flux density S. We assume that the point source is at the
phase center5.1and hence that in the absence of noise the visibility phase is zero.
Let the individual antenna gains5.2be G and system temperatures be T![]() and T
and T![]() . If
. If
![]() and
and ![]() are the noise voltages of antennas
are the noise voltages of antennas ![]() and
and ![]() respectively,then
respectively,then
![]() , and
, and
![]() . Similarly if
. Similarly if ![]() and
and
![]() are the voltages induced by the incoming radiation from
the point source,
are the voltages induced by the incoming radiation from
the point source,
![]() . The
instantaneous correlator5.3 output is given by:
. The
instantaneous correlator5.3 output is given by:
![]() is hence an unbiased
estimator of the true visibility.
is hence an unbiased
estimator of the true visibility.
![]() for which we need to be able to
work out:
for which we need to be able to
work out:
![]() have a
joint gaussian distribution then:
have a
joint gaussian distribution then:
![]() and
and ![]() . We have:
. We have:
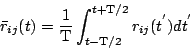
![]() . In this case, the signal to
noise ratio is:
. In this case, the signal to
noise ratio is:
![]() two element interferometers. Let us take
the case where the source is weak. Then from eqn(5.1.3) the
correlation between
two element interferometers. Let us take
the case where the source is weak. Then from eqn(5.1.3) the
correlation between ![]() and
and ![]() is given by
is given by
![]() and
and ![]() then
it can be shown that the noise in
then
it can be shown that the noise in ![]() and
and ![]() is
uncorrelated. Further
since the time averaging can be regarded as the adding together of a
large number of independent samples (
is
uncorrelated. Further
since the time averaging can be regarded as the adding together of a
large number of independent samples (
![]() ),
from the central limit theorem, the statistics of the noise in
),
from the central limit theorem, the statistics of the noise in
![]() and
and
![]() are well approximated as
Gaussian. It is then possible to derive the statistics of functions
of
are well approximated as
Gaussian. It is then possible to derive the statistics of functions
of
![]() and
and
![]() , such as the visibility
amplitude (
, such as the visibility
amplitude (
![]() ) and the visibility
phase (
) and the visibility
phase (
![]() ). For example, it
can be shown that the visibility amplitude has a Rice
distribution5.13
). For example, it
can be shown that the visibility amplitude has a Rice
distribution5.13
![]() in the image
plane is given by:
in the image
plane is given by: