Linear Arrays of n Elements of Equal Amplitude and Spacing :

Figure 6.2: Geometry for the n element array

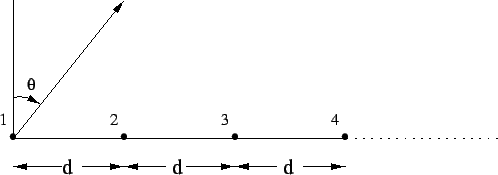
We now consider the case of a uniform linear array of n elements of equal amplitude, as shown in Figure 6.2. Taking the first element as the phase reference, the far field pattern is given by

$$E(\theta) ~~=~~ E_{0}~\left [1 ~+~ e^{j\psi} ~+~ e^{j2\psi} ~+~ \ldots ~+~ e^{j(n-1)\psi}\right ]~~~,$$ (6.2.3)

where $\psi = k\,d\,\sin{\theta} + \delta$ , $k = 2 \pi / \lambda$ is the wavenumber and $\delta$ is the progressive phase difference between the sources. The sum of this geometric series is easily found to be

$$E(\theta) ~~=~~ E_{0}~\frac {\sin(n\psi/2)} {\sin(\psi/2)} ~e^{j(n-1)\psi/2}.$$ (6.2.4)

If the centre of the array is chosen as the phase reference point, then the above result does not contain the phase term of $(n-1)\psi/2$. For nonisotropic but similar elements, $E_{0}$ is replaced by the element pattern, $E_{i}(\theta)$, to obtain the total field pattern.

The field pattern in eqn 6.2.4 has a maximum value of $nE_{0}$ when $\psi=0,2\pi,4\pi,\ldots ~$. The maxima at $\psi = 0$ is called the main lobe, while the other maxima are called grating lobes. For $d < \lambda$, only the main lobe maxima maps to the physically allowed range of $0 \leq \theta \leq 2\pi$. By suitable choice of the value of $\delta$, this maxima can be ``steered'' to different values of $\theta$, using the relation $k\,d\,\sin{\theta} = -\delta$. For example, when all the elements of the array are in phase ($\delta = 0$), the maximum occurs at $\theta = 0$. This is referred to as a ``broadside'' array. For a maximum along the axis of the array ( $\theta = 90^{o}$), $\delta = -k\,d$ is required, giving rise to an ``end-fire'' array. The broadside array produces a disc or fan shaped beam that covers a full 360$^{o}$ in the plane normal to the axis of the array. The end-fire array produces a cigar shaped beam which has the same shape in all planes containing the axis of the array. For nonisotropic elements, the element pattern also needs to be steered (electrically or mechanically) to match the direction of its peak response with that of the peak of the array pattern, in order to achieve the maximum peak of the total pattern.

For the case of $d > \lambda$, the grating lobes are uniformly spaced in $\sin{\theta}$ with an interval between adjacent lobe maxima of $\lambda/d$, which translates to $\geq \lambda/d$ on the $\theta$ axis (see Figure 6.3).

The uniform, linear array has nulls in the radiation pattern which are given by the condition $\psi = \pm 2\pi l/n, ~~l=1,2,3,\ldots$ which yields

$$\theta ~~=~~ \sin^{-1}\left[\frac {1}{kd} \left(\pm\frac {2\pi l}{n} - \delta\right)\right] ~~.$$ (6.2.5)

For a broadside array ($\delta = 0$), these null angles are given by

$$\theta ~~=~~ \sin^{-1}\left(\pm\frac {2\pi l}{nkd} \right) ~~.$$ (6.2.6)

Further, if the array is long ( $nd \gg l\lambda$), we get

$$\theta ~~\simeq~~ \pm ~\frac {\lambda l}{nd} ~~\simeq~~ \pm ~\frac {l}{L_{\lambda}} ~~,$$ (6.2.7)

where $L_{\lambda}$ is the length of the array in wavelengths and $L_{\lambda} \,=\, (n-1)d/\lambda \,\simeq\, nd/\lambda$ for large n. The first nulls occur at $l \,=\, \pm 1$, and the beam width between first nulls (BWFN) for such an array is given by

$$BWFN ~~=~~ \frac {2} {L_{\lambda}} ~rad ~~=~~ \frac {114.6} {L_{\lambda}} ~deg ~~.$$ (6.2.8)

The half-power beam width (HPBW) is then given by

$$HPBW ~~\simeq~~ \frac {BWFN} {2} ~~=~~ \frac {57.3} {L_{\lambda}} ~deg ~~.$$ (6.2.9)

Similarly, it can be shown that the HPBW of an end-fire array is $\sqrt{2/L_{\lambda}}$ (see ``Antennas'' by J.D. Kraus (1988) for more details).

Such linear arrays are useful for studying sources of size $< \lambda/d$ radians, as only one lobe of the pattern can respond to the source at a given time. Also, the source should be strong enough so that confusion due to other sources in the grating lobes is not significant. Linear grating arrays are particularly useful for studying strong isolated sources such as the Sun.

Figure 6.3: Grating lobes for an array of n identical elements. The solid line is the array pattern. The broad, dashed line curve is an example of the element pattern. The resultant of these two is shown as the dotted pattern.

The presence of grating lobes (with amplitude equal to the main lobe) in the response of an array is usually an unwanted feature, and it is desirable to reduce their levels as much as possible. For non-isotropic elements, the taper in the element pattern provides a natural reduction of the amplitude of the higher grating lobes. This is illustrated in Figure 6.3. To get complete cancellation of all the grating lobes starting with the first one, requires an element pattern that has periodic nulls spaced $\lambda/d$ apart, with the first null falling at the location of the first grating lobe. This requires the elements to have an aperture of $\sim \,d$, which makes the array equivalent to a continuous or filled aperture telescope. This can be seen mathematically by replacing $E_{0}$ in eqn 6.2.4 by the element pattern of an antenna of aperture size $d$ and showing that it reduces to the expression for the field pattern of a continuous aperture of size $nd$.

The theoretical treatment given above is easily extended to two dimensional antenna arrays.