The 2 Element Array

Figure 6.1: Geometry for the 2 element array.

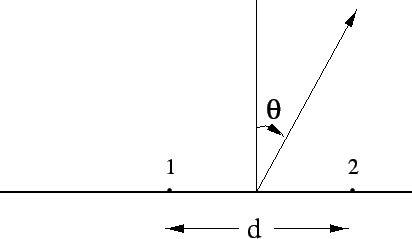
We begin by deriving the far field radiation pattern for the case of the simplest array, two isotropic point source elements separated by a distance d, as shown in Figure 6.1. The net far field in the direction $\theta$ is given as

$$E(\theta) ~~=~~ E_{1}~e^{j\psi/2} ~+~ E_{2}~e^{-j\psi/2} ~~~,$$ (6.2.1)

where $\psi = k\,d\,\sin{\theta} + \delta$ , $k = 2 \pi / \lambda$ is the wavenumber and $\delta$ is the intrinsic phase difference between the two sources. $E_{1}$ and $E_{2}$ are the amplitudes of the electric field due to the two sources, at the distant point under consideration. The reference point for the phase, referred to as the phase centre, is taken halfway between the two elements. If the two sources have equal strength, $E_{1} = E_{2} = E_{0}$ and we get

$$E(\theta) ~~=~~ 2\,E_{0}\,\cos(\psi/2)$$ (6.2.2)

The power pattern is obtained by squaring the field pattern. By virtue of the reciprocity theorem^6.1, $E(\theta)$ also represents the voltage reception pattern obtained when the signals from the two antenna elements are added, after introducing the phase shift $\delta$ between them.

For the case of $\delta = 0$ and $d \gg \lambda$, the field pattern of this array shows sinusoidal oscillations for small variations of $\theta$ around zero, with a period of $2\lambda/d$. Non-zero values of $\delta$ simply shift the phase of these oscillations by the appropriate value.

If the individual elements are not isotropic but have identical directional patterns, the result of eqn 6.2.2 is modified by replacing $E_{0}$ with the element pattern, $E_{i}(\theta)$. The final pattern is given by the product of this element pattern with the $\cos(\psi/2)$ term which represents the array pattern. This brings us to the important principle of pattern multiplication which can be stated as : The total field pattern of an array of nonisotropic but similar elements is the product of the individual element pattern and the pattern of an array of isotropic point sources each located at the phase centre of the individual elements and having the same relative amplitude and phase, while the total phase pattern is the sum of the phase patterns of the individual elements and the array of isotropic point sources. This principle is used extensively in deriving the field pattern for complicated array configurations, as well as for designing array configurations to meet specified field pattern requirements (see the book on ``Antennas'' by J.D. Kraus (1988) for more details).

Footnotes

... theorem^6.1

see Chapter 3