The Fourier transform of a signal ![]() is a decomposition
into frequency or spectral components. The DFT also performs a spectral
decomposition but with a finite spectral resolution. The spectrum
of a signal
is a decomposition
into frequency or spectral components. The DFT also performs a spectral
decomposition but with a finite spectral resolution. The spectrum
of a signal ![]() obtained using a DFT operation is the convolution of
the true spectrum of the signal
obtained using a DFT operation is the convolution of
the true spectrum of the signal ![]() convolved by the FT
convolved by the FT ![]() of
the window function, and sampled at discrete frequencies. Thus a DFT
is equivalent to a filter bank with filters spaced at
of
the window function, and sampled at discrete frequencies. Thus a DFT
is equivalent to a filter bank with filters spaced at ![]() in
frequency. The response of each filter is the Fourier transform
of the window function used to restrict the number of samples
to
in
frequency. The response of each filter is the Fourier transform
of the window function used to restrict the number of samples
to ![]() . For example, in the above analysis (see Section 8.3)
the response of each `filter' is the sinc function, (which
is the FT of the rectangular window
. For example, in the above analysis (see Section 8.3)
the response of each `filter' is the sinc function, (which
is the FT of the rectangular window ![]() ). The spectral resolution
(defined as the full width at half maximum (FWHM) of the filter response)
of the sinc function is
). The spectral resolution
(defined as the full width at half maximum (FWHM) of the filter response)
of the sinc function is
![]() . Different
window functions
. Different
window functions ![]() give different `filter' responses, i.e. for
give different `filter' responses, i.e. for
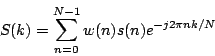 |
(8.3.5) |
| (8.3.6) | |||