next up previous contents
Next: Coordinate Transformation Up: Coordinate Systems Previous: Astronomical Co-ordinate System   Contents

Physical Coordinate System

The antennas are located on the surface and rotate with respect to a source in the sky due the rotation of the earth. For aperture synthesis the antenna positions are specified in a co-ordinate system such that the separation of the antennas is the projected separation in plane normal to the phase center. 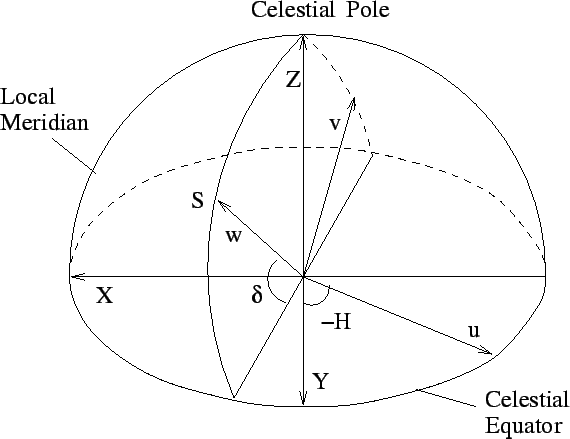In other words, in such a co-ordinate system the separation between the antennas is as seen by the observer sitting in the source reference frame. This system, shown in Fig 10.1, is the right-handed ($u,v,w$) coordinate system fixed on the surface of the earth at the array reference point, with the ($u,v$) plane always parallel to the tangent plane in the direction of phase center on the celestial sphere and the $w$ axis along the direction of phase center. The $u$ axis is along the astronomical E-W direction and $v$ axis is along the N-S direction. The ($u,v$) co-ordinates of the antennas are the E-W and N-S components of position vectors. As the earth rotates, the ($u,v$) plane rotates with the source in the sky, changing the ($u,v,w$) coordinates of the antennas, generating tracks in the $uv$-plane.

Figure 10.1: Relationship between the terrestrial co-ordinates (X,Y,Z) and the ($u,v,w$) co-ordinate system. The ($u,v,w$) system is a right handed system with the w axis pointing to the source S.
\begin{figure}\centerline{\epsfig{file=UVWCoords.eps, width=5.0in} }\end{figure}

In the above formulation, the $u$ co-ordinate of one antenna is with respect to the other antenna making the interferometer, which is located at the origin. If the origin is arbitrarily located and the co-ordinates of the two antennas are $u_1$ and $u_2$, Eq. 10.1.3 becomes

\begin{displaymath} r(u,l) = e^{2\pi\iota (u_1 - u_2) l}. \end{displaymath} (10.1.5)

Since only the relative positions of the antennas with respect to each other enter the equations, it is only useful to work with difference between the position vectors of various antennas in the ($u,v,w)$ co-ordinate system. The relative position vectors are called ``Baseline vectors'' and their lengths referred to as ``baseline length''.

The source surface brightness distribution is represented as a function of the direction cosines in the ($u,v,w$) coordinate system. In Eq. 10.1.4 above, $l$ is the direction cosine. The source coordinate system, which is flat only for small fields of view, is represented by ($l, m, n$). Since this coordinate system represents the celestial sphere, $n$ is not an independent coordinate and is constrained to be $n=\sqrt{1-l^2-m^2}$.

next up previous contents
Next: Coordinate Transformation Up: Coordinate Systems Previous: Astronomical Co-ordinate System   Contents
NCRA-TIFR