Below, we derive the generalized 2D Fourier transform relation between
the visibility and the source brightness distribution in the (![]() )
system. The geometery for this derivation is shown in Fig 10.3.
)
system. The geometery for this derivation is shown in Fig 10.3.
Let the vector ![]() represent the direction of the phase center
and the vector
represent the direction of the phase center
and the vector
![]() represent the location of all antennas
of an array with respect to a reference antenna. Then
represent the location of all antennas
of an array with respect to a reference antenna. Then
![]() . Note that
. Note that
![]() is phase by which the visibility should be rotated to stop the
fringe. For any source in direction
is phase by which the visibility should be rotated to stop the
fringe. For any source in direction
![]() ,
the output of an interferometer after fringe stopping will be
,
the output of an interferometer after fringe stopping will be
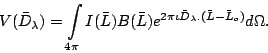 |
(10.2.8) |
If the array is such that all antennas are exactly located in the
(![]() ) plane,
) plane, ![]() is exactly zero and the above equation reduces to
an exact 2D Fourier transform relation between the source brightness
distribution and the visibility. This is true for a perfect east-west
array (like WSRT or ATCA). However to maximize the
is exactly zero and the above equation reduces to
an exact 2D Fourier transform relation between the source brightness
distribution and the visibility. This is true for a perfect east-west
array (like WSRT or ATCA). However to maximize the ![]() -coverage
arrays like GMRT or VLA are not perfectly east-west. As mentioned
earlier, the integrals in the above equation are finite for a small
portion of the sky (being limited by the primary beam patter of the
antennas). If the field of view being mapped is small (ie. for small
-coverage
arrays like GMRT or VLA are not perfectly east-west. As mentioned
earlier, the integrals in the above equation are finite for a small
portion of the sky (being limited by the primary beam patter of the
antennas). If the field of view being mapped is small (ie. for small
![]() and
and ![]() )
)
![]() and
can be neglected. Eq. 14.1.1 becomes
and
can be neglected. Eq. 14.1.1 becomes
Since there are finite number of antennas in an aperture synthesis
array, the ![]() -coverage is not continuous. Let
-coverage is not continuous. Let
| (10.2.11) |
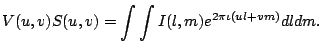 |
(10.2.12) |
Inverting the above equation and using the convolution theorem, we get
![]() where
where ![]() is the Fourier transform of
is the Fourier transform of ![]() .
. ![]() is the
transfer function of the the telescope for imaging and is referred to
as the Dirty Beam.
is the
transfer function of the the telescope for imaging and is referred to
as the Dirty Beam. ![]() represents the raw image produced by
an earth rotation aperture synthesis telescope and is referred to as
the Dirty Map. Contribution of Dirty Beam to the map and
methods of removing these these effects will be discussed in greater
detail in later lectures.
represents the raw image produced by
an earth rotation aperture synthesis telescope and is referred to as
the Dirty Map. Contribution of Dirty Beam to the map and
methods of removing these these effects will be discussed in greater
detail in later lectures.
In all the above discussion, we have assumed the observations are
monochromatic with negligible frequency bandwidth and that the (![]() )
measurements are instantaneous measurements. None of these assumptions
are true in real life. Observations for continuum mapping are made
with as large a frequency bandwidth as possible (to maximize the
sensitivity) and the data is recorded after finite integration. Both
result into degradation in the map plane and these effects will be
discussed in the later chapters.
)
measurements are instantaneous measurements. None of these assumptions
are true in real life. Observations for continuum mapping are made
with as large a frequency bandwidth as possible (to maximize the
sensitivity) and the data is recorded after finite integration. Both
result into degradation in the map plane and these effects will be
discussed in the later chapters.
Neglecting the ![]() -term essentially implies that the source brightness
distribution is approximated to be restricted to the tangent plane at
the phase center in the sky rather than on the surface of the
celestial sphere. At low frequencies, where the antenna primary beams
are larger and the radio emission from sources is also on a larger
scale, this assumption restricts the mappable part of the sky to a
fraction of the primary beam. Methods to relax this assumption will
also be discussed in a later lecture.
-term essentially implies that the source brightness
distribution is approximated to be restricted to the tangent plane at
the phase center in the sky rather than on the surface of the
celestial sphere. At low frequencies, where the antenna primary beams
are larger and the radio emission from sources is also on a larger
scale, this assumption restricts the mappable part of the sky to a
fraction of the primary beam. Methods to relax this assumption will
also be discussed in a later lecture.