The Measurement Equation

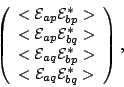
In this section we will develop a mathematical formulation useful for polarimetric interferometry. The theoretical framework is the van Cittert-Zernike theorem, which was discussed in chapter 2 in the context of the reconstruction of the Stokes I parameter of the source. However, as can be trivially verified, the theorem holds good for any of the Stokes parameters. So, apart from the issues of spurious polarization produced by propagation or instrumental effects, making maps of the Q, U, and V Stokes parameters is in principle^15.8 identical to making a Stokes I map.

Not surprisingly, matrix notation leads to an elegant formulation for polarimetric interferometry^15.9. Let us begin by defining a coherency vector,

$$\left( \begin{array}{c} <\mathcal{E}_{ap}\mathcal{E}^*_{bp}>... ...}>\\ <\mathcal{E}_{aq}\mathcal{E}^*_{bq}> \end{array}\right),$$

where $a, b$ refer to the two antennas which compose any given baseline, and $p,q$ are the two polarizations measured by the antenna. The coherency vector can be expressed as an outer product of the electric field, viz:

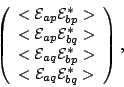
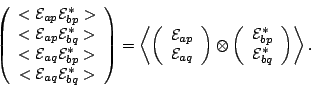$$\left( \begin{array}{c} <\mathcal{E}_{ap}\mathcal{E}^*_{bp}... ...E}^*_{bp} \\ \mathcal{E}^*_{bq}\\ \end{array}\right) \right>.$$ (15.3.10)

The Stokes vector can be obtained by multiplying the coherency vector with the Stokes matrix, (S). In a linear polarized co-ordinate system the components are:

$$\left(\begin{array}{c} I \\ Q \\ U \\ V\\ \end{array}\right)... ...\ <\mathcal{E}_{ay}\mathcal{E}^*_{by}>\\ \end{array}\right).$$ (15.3.11)

The component form could also be written down in the circular polarized co-ordinate system, in which case the matrix S would be:

$$\left(\begin{array}{c} I \\ Q \\ U \\ V\\ \end{array}\right)... ...\ <\mathcal{E}_{al}\mathcal{E}^*_{bl}>\\ \end{array}\right).$$ (15.3.12)

The matrix in equation (15.3.12) is related to that in equation (15.3.11) by a simple permutation of rows, as expected.

The outer product has the following associative property, viz. for matrices, A,B, C, and D,

$$({\bf A B})\otimes ({\bf C D}) = ({\bf A}\otimes {C})({\bf B}\otimes {D}).$$

For any one antenna $a$, putting in all the various effects discussed in section(15.2) we can write the voltage at the antenna terminals as:

$$\begin{array}{lcl} {\mathcal V}_a &=& {\bf G}_a {\bf B}_a {\... ...}_a {\mathcal E}_a\\ &=& {\bf J}_a \mathcal{E}_a. \end{array}$$ (15.3.13)

where,

$\mathcal{V}_a$	=	the voltage vector at the terminals of antenna $a$
${\bf G}_a$	=	the complex gain of the receivers of antenna $a$
${\bf B}_a$	=	the voltage beam matrix for antenna $a$
${\bf P}_a$	=	the parallactic angle matrix for antenna $a$
${\bf F}_a$	=	the Faraday rotation matrix for antenna $a$
$\mathcal{E}_a$	=	the electric field vector at antenna $a$
${\bf J}_a$	=	the Jones matrix for antenna $a$

The Jones matrix has been so called because of its analogy with the Jones matrix in optical polarimetry. All of these matrices are $2 \times 2$. In the linear polarized co-ordinate system. For example, we have:

$$\begin{array}{ll} {\bf F} = \left( \begin{array}{rr} \cos\ch... ...n{array}{rr} g_p & 0 \\ 0 & g_q \end{array}\right). \end{array}$$ (15.3.14)

The Jones matrix in polarimetric interferometry plays the same role as the complex gain does in scalar interferometry. Consequently one could conceive of schemes for self-calibration, since for an array with a large enough number of antennas sufficient number of closure constraints are available. However, since astrophysical sources are usually only weakly polarized, the signal to noise ratio in the cross-hand correlation products is often too low to make use of these closure constraints.

In scalar interferometry, phase fluctations caused by the atmosphere and/or ionosphere were lumped together with the instrumental gain fluctuations. In the vector formulation however, this is strictly speaking not possible, since these corrections occur at different points along the signal path, (see equations (15.3.13)) and matrices in equations (15.3.14) do not in general commute. However, for most existing radio telescopes, and for sources small compared to the primary beam, the matrices in equations (15.3.14) (apart from the Faraday rotation and Parallactic angle matrices) differ from the identity matrix only to first order (i.e. the off diagonal terms are small compared to the diagonal terms, and the diagonal terms are equal to one another to zeroth order), and consequently these matrices commute to first order. To first order hence, it is correct to lump the phase differences accumulated at different points along the signal path into the receiver gain. Alternatively, if we make the (reasonable) assumption that the complex atennuation (i.e. any absorption and phase fluctuation) produced by the atmosphere is identical for both polarizations, then it can be modeled as a constant times the identity matrix. Since the identity matrix commutes with all the other matrices, this factor can be absorbed in the receiver gain matrix, exactly as was done when dealing with interferometry of scalar fields. This is the reason why no separate matrix was introduced in equation (15.3.13) to account for atmospheric phase and amplitude fluctuations.

The matrix B in this formulation also deserves some attention. It simply contains the information on the relation between the electric field falling on the source and the voltage generated at the antenna terminals. It is an extension of the voltage beam in scalar field theory, and each element in the matrix depends on the sky co-ordinates $(l,m)$. As described above in section( 15.2), it is traditional to decompose it into a part which does not depend on $(l,m)$, which is called the leakage (or in the matrix formulation, the leakage matrix ``D''), and a part which depends on $(l,m)$. Provided that the leakage terms are small compared to the parallel hand antenna voltage gain, it can be shown that this decomposition is unique to first order.

In terms of the Jones matrix, the measured visibility on a single baseline for a point at the phase center can be written as:

$$\left(\begin{array}{c} \mathcal{V}_I \\ \mathcal{V}_Q \\ \... ... \left(\begin{array}{c} I \\ Q \\ U \\ V\\ \end{array}\right).$$ (15.3.15)

Note that this is a matrix equation, valid in all co-ordinate frames, i.e. it holds regardless of whether the antennas are linear polarized or circular polarized. In fact it holds even if some of the antennas are linear polarized, and the others are circular polarized.

If the point source were not at the phase center, then the visibility phase is not zero, and in equation (15.3.15), one would have to pre-multipy the Jones matrices with a matrix containing the Fourier kernel, viz. ${\bf K}_a(l,m)$, and ${\bf K}_b(l,m)$defined as:

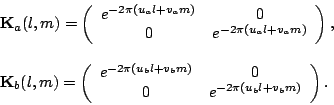$$\begin{array}{l} {\bf K}_a(l,m) = \left(\begin{array}{cc}e^{... ... & e^{-2\pi(u_b l + v_b m)} \\ \end{array} \right). \end{array}$$ (15.3.16)

To get the visibility for an extended incoherent source, one would have to integrate over all $(l,m)$, thus recovering the vector formulation of the van Cittert-Zernike theorem. In order to invert this equation, it is necessary not only to do the inverse fourier transform, but also to correct for the various corruptions introduced, i.e. the data has to be calibrated. The rest of this chapter discusses ways in which this polarization calibration can be done.

Footnotes

... principle^15.8

apart from the fact that one has to record four correlation functions, $<\mathcal{E}_{ap}\mathcal{E}^*_{bp}>$, $<\mathcal{E}_{ap}\mathcal{E}^*_{bq}>$, $<\mathcal{E}_{aq}\mathcal{E}^*_{bp}>$, $<\mathcal{E}_{aq}\mathcal{E}^*_{bq}>$, where $a, b$ refer to the two antennas which compose any given baseline, and $p,q$ are the two polarizations measured by the antenna. Since Stokes I maps are often all that is required, many observatories, including the GMRT, make a trade off such that fewer spectral channels are available if you record all four correlation products, than if you recorded only the two correlation products which are required for Stokes I.

... interferometry^15.9

Although this formulation has been in use in the field of optical polarimetry for decades, it was not appreciated until recently (Hamaker et al. 1996, and Sault et al. 1996) that it is also extendable to radio interferometric arrays.