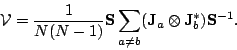Polarization Calibration

We restrict our attention to a point source at the phase center^15.10. The visibility that we measure, averaged over all baselines is

$$\mathcal{ V} = {1 \over N(N-1) } {\bf S} \sum_{a \ne b} ({\bf J}_a \otimes {\bf J}^*_b) {\bf S}^{-1}.$$ (15.4.17)

Any system describable by a Jones matrix is non-depolarizing^15.11 In the general case however, the summation in equation (15.4.17) cannot be represented by a single Jones matrix, and an interferometer is not therefore a non-depolarizing system. However, ideally, after calibration, the effective Jones matrices are all the unit matrix, and the interferometer would then be non-depolarizing.

Intuitively, it is clear that if one looks at an unpolarized calibrator source, one should be able to solve for the leakage terms, (which will produce apparent polarization) but that some degrees of freedom would remain unconstrained. Further it is also intuitive that the degrees of freedom which remain unconstrained are the following: (1) The absolute orientation of the feeds, (2) The intrinsic polarization of the feeds (i.e. for example, are they linear polarized or circular polarized?) and (3) The phase difference between the two polarizations. While one would imagine that the situation may be improved by observation of a polarized source, it turns out that this too is not sufficient to determine all the free parameters. What is required is observations of at least three differently polarized sources. For alt-az mounted dishes, the rotation of the beam with respect to the sky changes the apparent polarization of the source. For such telescopes hence, it is sufficient to observe a single source at several, sufficiently different hour angles. This is the polarization strategy that is commonly used at most telescopes. Faraday rotation due to the earth's ionosphere is more difficult to correct for. In principle models of the ionosphere coupled with a measure of the total electron content at the time of the observation can be used to apply a first order correction to the data.

We end this chapter with a brief description of the effect of calibration errors on the derived Stokes parameters. When observing with linearly polarized feeds, from equation (15.1.2) it is clear that if one observes a linearly polarized calibrator, the parallel-hand correlations will contain a contribution due to the Q component of the calibrator flux. Consequently, if one assumes (erroneously) that the calibrator was unpolarized the gain of the X channel will be overestimated and that of the Y channel underestimated. For this reason, for observations which require only measurement of Stokes I, circular feeds are preferable, since the Stokes V component of most calibrators is negligible, and consequently, measurements of the parallel hand correlations^15.12are sufficient to measure the correct Stokes I flux.

It is easy to show, that (to first order) if one observes a polarized calibrator with an error free linearly polarized interferometer and solves for the instrumental parameters under the assumption that the calibrator is unpolarized, the derived instrumental parameters of all the antennas will be in error by^15.13:

$$\begin{array}{ll} \begin{array}{lcl} \Delta g_x &=& +Q /2I \... ...egin{array}{lcl} d_y &=& {-(U-iQ) / 2I}. \end{array}\end{array}$$

where:

$\Delta g_x$		is the gain error of the X channel.
$\Delta g_y$		is the gain error of the Y channel.
$d_x$		is the leakage from the Y channel to the X channel.
$d_y$		is the leakage from the X channel to the Y channel.

If these calibration solutions are then applied to an unpolarized target source, then the source will appear to be polarized, with the same polarization percentage as the calibrator, but opposite sense. This again is simply the extension from scalar interferometry that if the calibrator flux is in error by some amount, the derived target source flux will be in error by the same fractional amount, but with opposite sense.

Footnotes

... center^15.10

For VLBI observations this is a very good approximation, since the source being imaged is very small compared to the primary beams of any of the antennas in the VLBI array.

... non-depolarizing^15.11

This follows trivially from the fact that for 100% polarization we must have $\mathcal{E}_p = c \mathcal{E}_q$, where $p,q$ are any two orthogonal polarizations, and $c$ is some complex constant. Multiplication by the Jones matrix will preserve this relationship (only changing the value of the constant $c$) thus producing another 100% polarized wave.

... correlations^15.12

recall from equations (15.1.3) that when $V=0$, $<\mathcal{E}_r\mathcal{E}^*_r> + <\mathcal{E}_l\mathcal{E}^*_l> = I$.

... by^15.13

A similar result can of course be derived for the case of circularly polarized antennas, the only difference will be the usual transpositions of $Q,U,$ and $V$.