Properties of the Gaussian

The general statement of gaussianity is that we look at the joint distribution of $N$ amplitudes $x_1=E(t_1), x_2=E(t_2), \ldots$ etc. This is of the form

$$P(x_1 \ldots x_k)=const \times \exp\left(-Q(x_1, x_2, \ldots x_k)\right)$$

Q is a quadratic expression which clearly has to increase to $+\infty$ in any direction in the $k$ dimensional space of the $x$'s. For just one amplitude,

$$P(x_1)=\frac{1}{\sigma\sqrt{2\pi}}e^{-x_1^2/2\sigma^2}$$

does the job and has one parameter, the ``Variance''$\sigma$, the mean being zero. This variance is a measure of the power in the signal. For two variables, $x_1$ and $x_2$, the general mathematical form is the ``bivariate gaussian''

$$P(x_1, x_2)= const \times \exp\left(-\frac{1}{2}(a_{11}x^2_1+2a_{12}x_1x_2+a_{22}x^2_2)\right)$$

.

Such a distribution can be visualised as a cloud of points in $x_1-x_2$ space, whose density is constant along ellipses $Q=$constant (see Fig. 1.2).

Figure 1.2: Contour lines of a bivariate gaussian distribution

The following basic properties are worth noting (and even checking!).

1. We need $a_{11}, a_{22},$ and $a_{11}a_{22}-a^2_{12}$ all $>0$  to have ellipses for the contours of constant $P$ ( hyperbolas or parabolas would be a disaster, since $P$ would not fall off at infinity).

2. The constant in front is
   
   $$\left(1/2\pi\right)\times \sqrt{det \left\vert \begin{array}{... ...a_{11} & a_{12} \\ a_{12} & a_{22} \\ \end{array} \right\vert }$$
   
   

3. The average values of $x_1^2, x^2_2$ and $x_1x_2$, when arranged as a matrix (the so called covariance matrix) are the inverse of the matrix of a's. For example,
   
   $$\langle x_1^2\rangle= a_{22}/det A$$
   
   
   
   
   $$\langle x_1 x_2\rangle= a_{12}/det A$$
   
   
   etc.

4. By time stationarity,
   
   $$<x^2_1>=<x^2_2>=\sigma^2$$
   
   
   
   
   $$<x^2_1>=<x^2_2>=\sigma^2$$
   
   

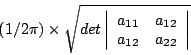
   The extra information about the correlation between $x_1$ and $x_2$ is contained in $<x_1x_2>$, i.e. in $a_{12}$ which (again by stationarity) can only be a function of the time separation $\tau=t_1-t_2$. We can hence write $<E(t)E(t+\tau)>=C(\tau)$ independent of $t$. $C(\tau)$ is called the autocorrelation function. From (1) above, $C^2(\tau) \le \sigma^2$. This suggests that the quantity $r(\tau)=C(\tau)/\sigma ^2$ is worth defining, as a dimensionless correlation coefficient, normalised so that $r(0)=1$. The generalisation of all these results for a $k$ variable gaussian is given in the Section 1.8