So far, we have only asserted that the sum of waves with
random phases generates a time-stationary gaussian signal. We now have to
check this. It is convenient to start with a signal going from ![]() to
to ![]() , and
only later take the limit
, and
only later take the limit
![]() . The usual theory of
Fourier series tells us that we can write
. The usual theory of
Fourier series tells us that we can write
where,
Notice that the frequencies come in multiples of the ``fundamental''
![]() which is very small since
which is very small since ![]() is large, and
hence they form a closely spaced set. We can now compute the
autocorrelation
is large, and
hence they form a closely spaced set. We can now compute the
autocorrelation
The averaging on the right hand side has to be carried out by
letting each of the phases ![]() vary independently from
vary independently from ![]() to
to
![]() . When we do this, only terms with
. When we do this, only terms with ![]() can survive, and we get
can survive, and we get
Putting ![]() equal to zero, we get the variance
equal to zero, we get the variance
We note that the autocorrelation is independent of ![]() and hence we have
checked time stationarity, at least for this statistical property. We now
have to face the limit
and hence we have
checked time stationarity, at least for this statistical property. We now
have to face the limit
![]() . The number of frequencies
in a given range
. The number of frequencies
in a given range ![]() blows up as
blows up as
Clearly, the ![]() have to scale inversely with
have to scale inversely with ![]() if statistical
qualities like
if statistical
qualities like ![]() are to have a well defined
are to have a well defined
![]() behaviour. Further, since the number of
behaviour. Further, since the number of ![]() 's even in a small interval
's even in a small interval
![]() blows up, what is important is their combined effect rather
than the behaviour of any individual one. All this motivates the definition.
blows up, what is important is their combined effect rather
than the behaviour of any individual one. All this motivates the definition.
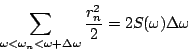
as
![]() Physically,
Physically,
![]() is the
contribution to the variance
is the
contribution to the variance
![]() from the interval
from the interval
![]() to
to
![]() . Hence the term ``power spectrum'' for
. Hence the term ``power spectrum'' for
![]() . Our basic result for the autocorrelation now reads
. Our basic result for the autocorrelation now reads
if we define
![]() .
.
This is the ``Wiener-Khinchin theorem'' stating that the autocorrelation
function is the Fourier transform of the power spectrum. It can also be
written with the frequency measured in cycles (rather than radians) per
second and denoted by ![]() .
.
and as before,
![]() .
.
In this particular case of the autocorrelation, we did not use
independence of the ![]() 's. Thus the theorem is valid even for a
non-gaussian random process. (for which different
's. Thus the theorem is valid even for a
non-gaussian random process. (for which different ![]() 's are not
independent). Notice also that we could have averaged over
's are not
independent). Notice also that we could have averaged over ![]() instead of over all the
instead of over all the ![]() 's and we would have obtained the same
result, viz. that contributions are nonzero only when we multiply a given
frequency with itself. One could even argue that the operation of integrating
over the
's and we would have obtained the same
result, viz. that contributions are nonzero only when we multiply a given
frequency with itself. One could even argue that the operation of integrating
over the ![]() 's is summing over a fictitious collection (i.e ``ensemble'') of
signals, while integrating over
's is summing over a fictitious collection (i.e ``ensemble'') of
signals, while integrating over ![]() and dividing by
and dividing by ![]() is closer to what
we do in practice. The idea that the ensemble average can be realised by
the more practical time average is called ``ergodicity'' and like everything
else here, needs better proof than we have given it.
A rigorous treatment would in fact start by worrying about
existence of a well-defined
is closer to what
we do in practice. The idea that the ensemble average can be realised by
the more practical time average is called ``ergodicity'' and like everything
else here, needs better proof than we have given it.
A rigorous treatment would in fact start by worrying about
existence of a well-defined
![]() limit for all statistical
quantities, not just the autocorrelation. This is called ``proving the
existence of the random process''.
limit for all statistical
quantities, not just the autocorrelation. This is called ``proving the
existence of the random process''.
The autocorrelation ![]() and the power spectrum
and the power spectrum ![]() could in
principle be measured in two different kinds of experiments. In the time
domain, one could record samples of the voltage and calculate averages of
lagged products to get
could in
principle be measured in two different kinds of experiments. In the time
domain, one could record samples of the voltage and calculate averages of
lagged products to get ![]() . In the frequency domain one would pass the
signal through a filter admitting a narrow band of frequencies around
. In the frequency domain one would pass the
signal through a filter admitting a narrow band of frequencies around
![]() , and measure the average power that gets through.
, and measure the average power that gets through.
A simple but instructive application of the Wiener Khinchin theorem is to
a power spectrum which is constant (``flat band'') between ![]() and
and
![]() . A simple calculation shows that
. A simple calculation shows that
The first factor ![]() is the value at
is the value at ![]() , hence the total
power/variance to radio astronomers/statisticians. The second factor is
an oscillation at the centre frequency. This is easily understood. If the
bandwidth
, hence the total
power/variance to radio astronomers/statisticians. The second factor is
an oscillation at the centre frequency. This is easily understood. If the
bandwidth ![]() is very small compared to
is very small compared to ![]() , the third factor would be
close to unity for values of
, the third factor would be
close to unity for values of ![]() extending over say
extending over say ![]() , which is
still many cycles of the centre frequency. This approaches the limiting
case of a single sinusoidal wave, whose autocorrelation is sinusoidal.
The third sinc function factor describes ``bandwidth decorrelation1.1'', which occurs
when
, which is
still many cycles of the centre frequency. This approaches the limiting
case of a single sinusoidal wave, whose autocorrelation is sinusoidal.
The third sinc function factor describes ``bandwidth decorrelation1.1'', which occurs
when ![]() becomes comparable to or larger than
becomes comparable to or larger than ![]() .
.
Another important case, in some ways opposite to the preceding one,
occurs when ![]() , so that the band extends from
, so that the band extends from ![]() to
to ![]() . This
is a so-called ``baseband''. In this case, the autocorrelation is proportional
to a sinc function of
. This
is a so-called ``baseband''. In this case, the autocorrelation is proportional
to a sinc function of ![]() . Now, the correlation between a pair of
voltages measured at an interval of
. Now, the correlation between a pair of
voltages measured at an interval of ![]() or any multiple (except zero!)
thereof is zero, a special property of our flat band. In this case, we see
very clearly that a set of samples measured at this interval of
or any multiple (except zero!)
thereof is zero, a special property of our flat band. In this case, we see
very clearly that a set of samples measured at this interval of ![]() ,
the so-called ``Nyquist sampling interval'', would actually be statistically
independent since correlations between any pair vanish (this would be
clearer after going through Section 1.8). Clearly, this is the minimum
number of measurements which would have to be made to reproduce the signal,
since if we missed one of them the others would give us no clue about it.
As we will now see, it is also the maximum number for this bandwidth!
,
the so-called ``Nyquist sampling interval'', would actually be statistically
independent since correlations between any pair vanish (this would be
clearer after going through Section 1.8). Clearly, this is the minimum
number of measurements which would have to be made to reproduce the signal,
since if we missed one of them the others would give us no clue about it.
As we will now see, it is also the maximum number for this bandwidth!