Delay Tracking and Fringe Stopping

Signals received by antennas are down converted to baseband by mixing with a local oscillator of frequency $\nu_{LO}$. The geometric delay compensation is usually done by introducing delays in the baseband signal. The output of a correlator after introducing a delay $\tau_i$ can be written as (see Chapter 4)

$$r_R(\tau_g) = \vert{\cal V}\vert \cos(2\pi\nu\tau_g - 2\pi\nu_{BB}\tau_i + \Phi_{\cal V})$$ (9.1.2)

$$= \vert{\cal V}\vert \cos(2\pi\nu_{LO}\tau_g - 2\pi\nu_{BB}\Delta\tau_i + \Phi_{\cal V})\;,$$ (9.1.3)

where $\nu_{BB}$ is the baseband frequency and $\Delta\tau_i = \tau_g - \tau_i$ is the residual delay. There are two terms that arise in the equation due to delay compensation:

1. $2\pi\nu_{BB}\Delta\tau_i$, and
2. $2\pi\nu_{LO}\tau_g$.

The first term is due to finite precision of delay compensation and the later is a consequence of the delay being compensated in the baseband (as opposed to the RF, which is where the geometric delay is suffered, see Chapter 4). The phase $2\pi\nu_{BB}\Delta\tau_i$ depends on $\nu_{BB}$. For observations with a bandwidth $\Delta \nu$ this term produces a phase gradient across $\Delta \nu$. The phase gradient is a function of time since the delay error changes with time. The phase $2\pi\nu_{LO}\tau_g$ is independent of $\nu_{BB}$, thus is a constant across the entire band. This phase is also a function of time due to time dependence of $\tau_g$. Thus both these quantities have to be dynamically compensated.

Figure 9.1: Digital implementation of delay tracking in units of the sampling period using shift registers (top) and random access memory (bottom).

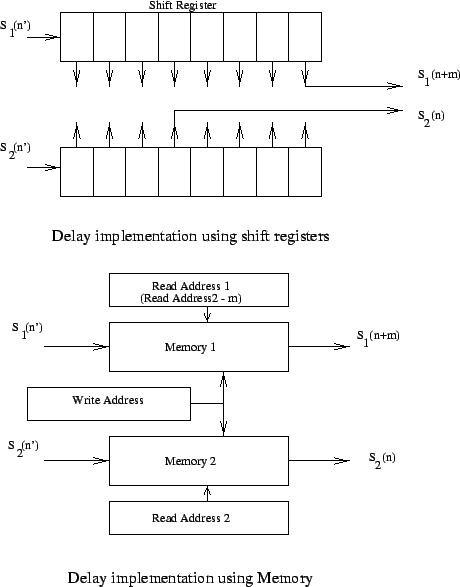Delay compensation in multiples of sampling interval $1/f_s$ can be achieved by shifting the sampled data (see Chapter 8). This is schematically shown in Fig. 9.1. The digitized samples are passed through shift registers. The length of the shift registers are adjusted to introduce the required delay between the signals. Another way of implementing delay is by using random access memory (RAM). In this scheme, the data from the antennas are written into a RAM (Fig. 9.1). The data is then read out from this memory for further proccessing. However, the read pointer and the write pointer are offset, and the offset between the two can be adjusted to introduce exactly the required delay. In the GMRT correlator, the delay compensation is done using such a high speed dual port RAM.

A fractional delay can be introduced by changing the phase of the sampling clock. The phase is changed such that signals from two antennas are sampled with a time difference equal to the fractional delay. A second method is to introduce phase gradients in the spectrum of the signal (see Chapter 8). This phase gradient can be introduced after taking Fourier Transforms of signals from the antennas (see Section 9.2.1).

Compensation of $2\pi\nu_{LO}\tau_g$, (called fringe stopping, can be done by changing the phase of the local oscillator signal by an amount $\phi_{LO}$ so that $2\pi\nu_{LO}\tau_g - \phi_{LO} = 0$. Alternatively, this compensation can be achieved digitally by multiplying the sampled time series by $e^{-j\phi_{LO}}$. (Recall from above that the fringe rate is the same for all frequency channels, so this correction can be done in the time domain). The fringe

$$\phi_{LO}(t) = 2\pi\nu_{LO}\tau_g = 2\pi\nu_{LO}\frac{b\sin({\Omega t})}{c}$$ (9.1.4)

is a non-linear function of time (see Chapter 4). Here $\Omega$ is the rate at which the source is moving in the sky (i.e. the angular rotation speed of the earth), $b$ is the baseline length and $c$ is the velocity of light. For a short time interval $\Delta t$ about $t_0$ the time dependence can be approximated as

$$\phi_{LO}(t) = \phi_{LO}(t_0) + 2\pi\nu_{LO}\frac{b\Omega\cos(\Omega t_0)}{c}\Delta t.$$ (9.1.5)

i.e. $\phi_{LO}(t)$ is the phase of an oscillator with frequency

$$\nu_{LO}\frac{b\Omega\cos(\Omega t_0)}{c}$$ (9.1.6)

After a time interval $\Delta t$ the frequency of the oscillator has to be updated. Digital implementation of an oscillator of this type is called a Number controlled oscillator (NCO). The frequency of the oscillator is varied by loading a control $number$ to the device. The initial phase of the NCO can also be controlled which is used to introduce $\phi_{LO}(t_0)$. In the GMRT correlator, fringe stopping is done using an NCO.