


Next: Delay Tracking and Fringe
Up: General Theory
Previous: Further Reading
Contents
Correlator - II: Implementation
D. Anish Roshi
The visibility measured by an interferometer is characterized
by the amplitude and phase of the fringe at different instants. For
simplicity first consider the output of a two element interferometer.
In the quasi monochromatic approximation the multiplier output can be
written as (see Chapter 4)
![\begin{displaymath}
r_R(\tau_g) = \mbox{Re}[v_1(\nu,t)v^*_2(\nu,t)] = \vert{\cal V}\vert \cos (2\pi\nu\tau_g + \Phi_{\cal V}),
\end{displaymath}](img905.gif) |
(9.0.1) |
where 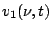 and
and 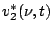 are the voltages at the outputs of the
receiver systems of the two antennas,
are the voltages at the outputs of the
receiver systems of the two antennas, 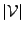 and
and 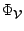 are the
amplitude and the phase of the visibility and
are the
amplitude and the phase of the visibility and 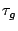 is the geometric delay.
The quantities required for mapping a source are
is the geometric delay.
The quantities required for mapping a source are 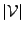 and
and
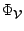 for all pairs of antennas of the interferometer. These
quantities are measured by first canceling the
for all pairs of antennas of the interferometer. These
quantities are measured by first canceling the 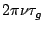 term in
Eq. 9.0.1 by delay tracking and fringe stopping. In general,
one needs to know the amplitude and phase of the visibility as a function of
frequency. This chapter covers the implementation of a spectral
correlator to measure the visibility amplitude and phase. Further since
the delay tracking (and fringe stopping for some cases) is usually also
done by the correlator, these issues are also discussed.
term in
Eq. 9.0.1 by delay tracking and fringe stopping. In general,
one needs to know the amplitude and phase of the visibility as a function of
frequency. This chapter covers the implementation of a spectral
correlator to measure the visibility amplitude and phase. Further since
the delay tracking (and fringe stopping for some cases) is usually also
done by the correlator, these issues are also discussed.
Subsections



Next: Delay Tracking and Fringe
Up: General Theory
Previous: Further Reading
Contents
NCRA-TIFR