Solution for the complex gains

3 Solution for the complex gains

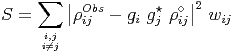
Assuming that the antenna dependent complex gains are independent, with a gaussian probability density function (this implies that the real and imaginary parts are independently gaussian random processes), one can estimate g_is by minimizing, with respect to g_is, the function S given by

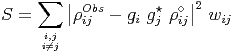∑ | | S = |ρOibjs- gi g⋆j ρ∘ij|2 wij i,j i⁄=j

(4)

where w_ij = 1∕σ_ij², σ_ij being the variance on the measurement of ρ_ij^Obs

Dividing the above equation by ρ_ij^∘ (the source model, which is presumed to be known - it is trivially known for an unresolved source), and writing ρ_ij^Obs∕ρ_ij^∘ = X_ij, we get

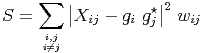∑ || ⋆||2 S = Xij - gi gj wij ii,j⁄=j

(5)

If ρ_ij^∘ represents the structure of the source accurately, X_ij will have no source dependent terms and is purely a product of the two antenna dependent complex gains.

Expanding Eq. 5, we get

∑ [ ] S = |Xij|2 - g ⋆igjXij - gig⋆jX ⋆ij + gig⋆igjg⋆j wij i,j i⁄=j

(6)

Evaluation ∂S _ ∂g_i^⋆ and equating it to zero ³, we get

∂S ∑ [ ] --⋆- = - gjXijwij + gigjg⋆jwij = 0 ∂gi j j⁄=i

(7)

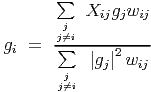∑ Xijgjwij jj⁄=i gi = ∑------2---- j |gj|wij j⁄=i

(8)

This can also be derived by equating the partial derivatives of S with respect to real and imaginary parts of g_i as shown in the appendix.

Since the antenna dependent complex gains also appear on the right-hand side of Eq. 8, it has to be solved iteratively starting with some initial guess for g_js or initializing them all to (1,0).

Eq. 8 can be written in the iterative form as:

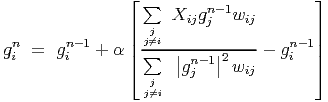⌊ ∑ n-1 ⌋ | j Xijg j wij | n n-1 | j⁄=i------------- n-1| gi = gi + α |⌈ ∑ ||gn-1||2w - gi |⌉ j j ij j⁄=i

(9)

where n is the iteration number and 0 < α < 1. Convergence would be defined by the constraint

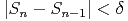|Sn - Sn-1| < δ

(10)

(the change in S from one iteration to another) where δ is the tolerance limit.

[next] [prev] [prev-tail] [front] [up]