Update direction in real and imaginary representation

A Update direction in real and imaginary representation

g_is are complex functions. One can therefore write S in terms of g_i^I and g_i^R, the real and imaginary parts of g_i and minimize with respect to g_i^I and g_i^R separately. It is shown here that the complex arithmetic achieves exactly this and the results are same as that given by complex calculus. The superscripts I and R in the following are used to represent the real and imaginary parts of complex quantities.

Expanding Eq. 5, ignoring w_ijs and writing it in terms of real and imaginary parts we get

∑ ∑ ||X - g g⋆||2 = [X - g g⋆][X ⋆ - g⋆g ] i,j ij i j i,j ij i j ij i j i⁄=j i⁄=j ∑ [( R I) ( R I)( R I)] = X ij + ιXij - gi + ιgi gj - ιgj i,i⁄=jj [( R I) ( R I)( R I) ] ∑ X ij - ιXij - gi - ιgi gj + ιgj = [(XR - gRgR - gIgI) + ι(XI + gRgI - gIgR )] i,j ij i j i j ij i j i j i⁄=j [(XR - gRgR - gIgI) - ι(XI + gRgI - gIgR )] ∑ ij i j i j ij i j i j = S0S ⋆0 i,j i⁄=j

(14)

where

[ ] [ ] S0 = XR - gR gR - gIgI + ι XI + gR gI- gIgR ij i j i j ij i j i j

(15)

Taking partial derivative of S with respect to g_i^R and reintroducing w_ij, we get

∑ ∂S--= { [- gR + ιgI] S⋆ - S [gR + ιgI]}w ∂gRi j j j 0 0 j j ij j⁄=i ∑ [ ⋆ ⋆] = - S0gj + g jS0 wij jj⁄=i ∑ = - 2 Re (S0gjwij) jj⁄=i ∑ [( ) ( ) ] = - 2 XRij - gRi gRj - gIigIj gRj + XIij + gRi gIj - gIigRj gIj wij j ∑j⁄=i[ ] = - 2 XRijgRj - XIijgIj - gRi gIj2 - gRi gRj 2 wij j j⁄=i

(16)

Therefore,

-∂S- ∑ [ 2 R ] ∂gR = - 2 Re (Xijgj) - |gj| gi wij i jj⁄=i

(17)

Equating ∂S _ ∂g_i^R to zero, we get

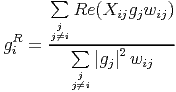∑ j Re (Xijgjwij) R -j⁄=i------------- gi = ∑ |g |2 w j j ij j⁄=i

(18)

Similarly

∂S-- ∑ [ 2 I] ∂gIi = - 2 Im (Xijgj) - |gj| gi wij jj⁄=i

(19)

Therefore the equivalent imaginary part of Eq. 18 is

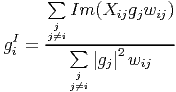∑ Im (X g w ) j ij j ij gI= j⁄=i∑------------- i |gj|2wij j j⁄=i

(20)

writing g_i = g_i^R + ιg_i^I and substituting for g_i^R and g_i^I from Eq. 18 and 20 respectively, we get

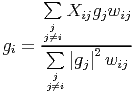∑ X g w j ij j ij gi = -j⁄=∑i--------- |gj|2wij jj⁄=i

(21)

This is same as Eq. 8, which was arrived at by evaluating a complex derivative of Eq. 5 as ∂S∕∂g_i^⋆, treating g_i and g_I^⋆ as independent variables. Evaluating ∂S ∂g_i = 0 would give the complex conjugate of Eq. 21. Hence, ∂S∕∂g_i gives no independent information not present in ∂S∕∂g_i^⋆.

[prev] [prev-tail] [front] [up]